Главная | Обратная связь

Бозе-Эйнштейна и Ферми-Дирака

 

Квантовая статистика – раздел статистической физики, исследующий системы, которые состоят из огромного числа частиц, подчиняющихся законам квантовой механики.

При рассмотрении системы многих частиц в классической статистической физике (распределения Максвелла и Больцмана) предполагалось, что частицу можно отличить от всех таких же частиц. Например, если две частицы поменяются местами, то получится новое микросостояние.

Квантовая статистика строится на принципе неразличимости тождественных частиц: все одинаковые частицы (например, все электроны в металлах, все протоны в ядрах атомов) считаются принципиально неразличимыми друг от друга. Если частицы поменяются местами друг с другом, то получится исходное микросостояние.

Напомним, что состояние электрона в атоме однозначно определяется набором четырех квантовых чисел: главного, орбитального, магнитного и магнитного спинового. Распределение электронов в атоме подчиняетсяпринципу Пáули: в одном и том же атоме не может быть более одного электрона с одинаковым набором четырех квантовых чисел.

Все элементарные частицы разделяются на два класса.

К одному классу относятся электроны, протоны, нейтроны и все частицы с полуцелым спином. Эти частицы подчиняются квантовой статистике Фéрми-Дирáка и поэтому называются фермиóнами. Фермионы подчиняются принципу Паули, и в данном квантовом состоянии не может находиться более одной частицы. (Аналогия: в одном месте пространства не может находиться больше одного непроницаемого твёрдого тела.)

К другому классу относятся фотоны, фононы, p- и К-мезоны и все частицы с целым спином. Системы таких частиц описываются квантовой статистикой Бóзе-Эйнштéйна и поэтому называются бозóнами. Бозоны не подчиняются принципу Паули: в каждом квантовом состоянии может находиться любое число частиц. (Аналогия: в одном месте пространства возможно одновременное пребывание облаков пара или дыма, лучей света, звуковых волн и радиоволн.)

Основной в квантовой статистике является задача о распределении частиц по координатам и скоростям (энергиям) и нахождении средних значений величин, характеризующих рассматриваемую систему. Для нахождения общего числа всех возможных квантовых состояний системы из N частиц вводится понятие 6N-мерного фазового пространства, так как состояние системы определяется заданием 6N переменных, поскольку состояние каждой частицы определяется тройкой координат x, y, z и тройкой соответствующих проекций импульса p_x, p_y, p_z.

Число частиц, которые могут находиться в одном квантовом состоянии, определяется числами заполнения N_i. Для бозонов числа заполнения могут принимать любые целые значения N_i = 0, 1, 2, 3... Для фермионов возможны только два числа: 0 для свободных состояний и 1 для занятых. Сумма всех чисел заполнения должна быть равна числу частиц в системе. Квантовая статистика позволяет подсчитать среднее число частиц в данном квантовом состоянии áN_iñ. Для этого были получены следующие функции распределения:

 

 

 

 

 

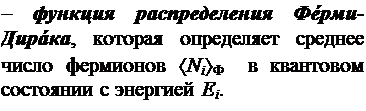
В этих формулах: k – постоянная Больцмана; Т – термодинамическая температура. Величина m = (U – TS + pV) / N называется химическим потенциалом, отнесённым к отдельной частице (U – внутренняя энергия системы; S – её энтропия; V – объём системы; р – давление).

Система частиц (в частности, газ) называется вырожденной, если её свойства существенным образом отличаются от свойств систем, подчиняющихся классической статистике. Параметром вырождения называется величина A = exp (m/kT ). При А << 1, т.е. при малой степени вырождения, в квантовых функциях распределений f_Б и f_Ф можно пренебречь единицей в знаменателях, и распределения Бозе-Эйнштейна и Ферми-Дирака переходят в классическое распределение Максвелла-Больцмана:

.

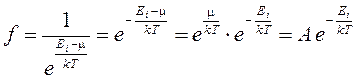Условие малости вырождения имеет вид

,

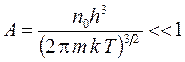где n₀ – концентрация частиц; m – масса частиц; k – постоянная Больцмана; h – постоянная Планка; Т – температура.

Температурой вырождения Т_В называется температура, при которой вырождение становится существенным. Ниже этой температуры отчётливо проявляются квантовые свойства системы частиц. Если Т >> Т_В, то поведение системы частиц (газа) описывается классическими законами. Температура вырождения определяется из условия А = 1.

Вырождение газов становится существенным при очень низких температурах и больших плотностях. Например, для водорода при нормальных условиях (Т = 300 К и n₀ » 3 ×10²⁵ м^-3) параметр вырождения А » 3 ×10^-5 << 1. Температура вырождения для водорода Т_В » 1 К. Для всех остальных газов, более тяжелых, чем водород, величина А еще меньше. Поэтому газы при нормальных условиях не бывают вырожденными и описываются классической статистикой Максвелла-Больцмана.

Электроны проводимости в металлах являются примером вырожденного газа. В обычных условиях n₀ » (10²⁸ -10²⁹) м^-3. Так как масса электрона мала (m » 10^-30 кг), то Т_В » 2000 К, т.е. для всех температур, при которых металл может существовать в твёрдом состоянии, электронный газ в металле вырожден. Поэтому среднее число электронов N(E), находящихся в квантовом состоянии с энергией Е, описывается функцией распределения Ферми-Дирака:

.

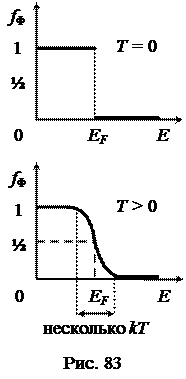
Для электронов (фермионов) среднее число частиц в квантовом состоянии и вероятность заполнения квантового состояния (от 0 до 1) совпадают.

Графики функций Ферми-Дирака для температур Т = 0 и Т > 0 показаны на рис. 83. Такое распределение обусловливается необходимостью соблюдения двух требований: во-первых, полная энергия должна быть минимальной, и, во-вторых, должен соблюдаться принцип Паули. Поэтому при Т = 0 все электроны не могут находиться на самом минимальном энергетическом уровне. Они начинают заполнять квантовые состояния с самого нижнего энергетического уровня, последовательно занимая более высокие квантовые состояния, причем каждое из них лишь одним электроном. Последний электрон занимает уровень с максимальной энергией. Этот уровень называется уровнем Ферми, а энергия уровня – энергией Фéрми Е_F. При Т = 0 функция разрывная. При E < E_F функция f_Ф = 1, т.е. все квантовые состояния с такими энергиями заполнены электронами. При E > E_F функция f_Ф = 0, т.е. все квантовые состояния свободны. При этом Е_F = m, и распределение Ферми-Дирака обычно записывается в виде

.

Однако такое наглядное определение энергии Ферми имеет смысл лишь в применении к свободным электронам в металле. В общем случае такое определение не точно. Например, в диэлектриках и во многих полупроводниках энергетический уровень Ферми располагается примерно в середине запрещенной зоны, где заведомо нет разрешенных энергетических уровней электронов. Поэтому более общее определение гласит: уровень Фéрми – это такой энергетический уровень, вероятность заполнения которого электроном равна 1/2. Это следует из последней формулы при подстановке в неё энергии Е равной E_F.

При температурах Т > 0 функция распределения f_Ф плавно изменяется («размывается») от 1 до 0 в узкой области (порядка нескольких kT ) в окрестности E_F. Причина такого «размытия» в том, что небольшая часть электронов получает дополнительную энергию за счёт взаимодействия с тепловыми колебаниями кристаллической решетки. Поскольку средняя энергия теплового движения атомов имеет порядок kT, то и область изменения энергии электронов вблизи уровня Ферми также имеет порядок нескольких kT. В самом деле, подсчитаем значение f_Ф(Е) для энергий Е, отличающихся от E_F на ±3kT (т.е. E – E_F = ±3kT):

; .

 

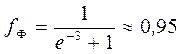30. КВАНТОВЫЕ ТЕОРИИ ТЕПЛОЁМКОСТИ

ЭЙНШТЕЙНА И ДЕБАЯ. ФОНОНЫ

 

Классическая теория теплоёмкости имеет ограниченное применение, так как её теоретические выводы не всегда согласуются с экспериментом.

Классическая теория не даёт объяснения зависимости теплоёмкости газов от температуры. Из простых формул для расчета теплоёмкостей (C_p = (i + 2) R/2 и C_V = iR/2) следует, что молярные теплоёмкости газов определяются лишь числом степеней свободы и не зависят от температуры. Это справедливо только для одноатомных и многих двухатомных газов (Н₂, О₂, N₂) при комнатной температуре. У трехатомных газов теоретические и экспериментальные результаты сильно отличаются.

Рассмотрим температурную зависимость теплоемкости C_V для водорода, показанную на рис. 84. Из графика видно, что при 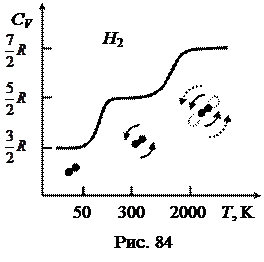повышении температуры проис­ходит как бы «включение» различных степеней свободы: при малой температуре включаются лишь поступательные степени свободы, а затем вращательные и колебательные. Это явление объясняет квантовая механика, согласно которой энергия может принимать не любое значение, а только дискретный ряд значений. Энергия может меняться только скачками. 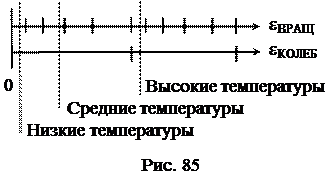Упро­щённая схема уровней энергии (вращательных и колебательных) схематически представлена на рис. 85. При низких температурах энергия теп­лового движения меньше разности энергий соседних уровней (kT << De), и при столкновениях молекул вращательные и колебательные степени свободы не возбуждаются. Поведение двухатомного газа подобно одноатомному. Так как разность между соседними вращательными уровнями энергии значительно меньше, чем между колебательными (De_ВРАЩ << De_КОЛЕБ), то с ростом температуры возбуждаются вначале вращательные степени свободы, в результате чего теплоёмкость возрастает; при дальнейшем росте температуры возбуждаются и колебательные степени свободы и происходит дальнейший рост теплоёмкости.

Плавные переходы на температурном графике C_V между дискретными уровнями (рис. 84) объясняются тем, что согласно распределению молекул по скоростям и энергиям лишь какая-то доля молекул от общего числа первоначально имеет энергию, достаточную для возбуждения вращательного и колебательного движений.

Согласно классической теории теплоёмкость металлов должна складываться из теплоёмкости кристаллической решетки, равной 3R (закон Дюлонга и Пти), и теплоёмкости электронного газа, равной 3R/2 (электрон как материальная точка имеет среднюю кинетическую энергию, равную 3kT/2). Таким образом, атомная теплоёмкость металлов должна быть близка к 4,5R. Однако опыт показывает, что она равна 3R. Это объясняет квантовая механика. Известно, что функции распределения Ферми-Дирака для Т = 0 и для Т > 0 различаются лишь в узкой области энергий порядка нескольких kT. Следовательно, в процессе нагревания металла участвует лишь незначительная доля от всех электронов проводимости. Поэтому отсутствует заметная разница между теплоёмкостями металлов и диэлектриков (»3R), что не могло быть объяснено классической теорией.

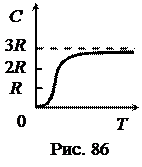Классическая теория теплоёмкости не объясняеттемпературную зависимость молярной теплоёмкости твёрдых тел, показанную на рис. 86, которая в области низких температур пропорциональна кубу температуры.

Простейшая квантовая теория была предложена Эйнштейном. В этой теории кристалл рассматривался как система N атомов, каждый из которых являлся квантовым гармоническим осциллятором. Колебания всех атомов происходят независимо друг от друга с одинаковой частотой n. Средняя энергия áeñ, приходящаяся на одну степень свободы атома квантового гармонического осциллятора, равна

.

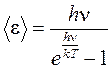Внутренняя энергия 1 моля твёрдого тела (с учетом 3 степеней свободы колебаний атома в узле решетки) выражается следующим образом:

.

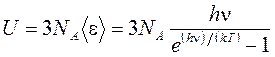Для нахождения молярной теплоёмкости необходимо взять производную:

 

.

Если ввести характеристическую температуру Эйнштейна

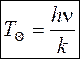, то .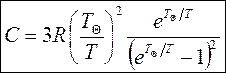

Полученная формула Эйнштейна лишь качественно описывает зависимость теплоёмкости твёрдых тел от температуры: при высоких температурах (hn << kT) теплоёмкость С ® 3R, а при Т ® 0 теплоёмкость С ® 0. Однако количественно поведение теплоемкости твёрдого тела вблизи абсолютного нуля описывается недостаточно точно.

Дебай развил упрощенную теорию Эйнштейна. В теории Дебая учтено, что колебания атомов в кристаллической решетке не являются независимыми. Между атомами твердого тела имеются настолько сильные взаимодействия, что все N частиц тела образуют связанную систему, обладающую 3N степенями свободы, причем колебания всех атомов могут происходить с разными частотами.

Рассматривая непрерывный спектр частот осцилляторов, Дебай показал, что основной вклад в среднюю энергию квантового осциллятора вносят колебания низких частот, соответствующих упругим волнам звукового (или ультразвукового) диапазона. Связь между частицами в кристаллической решетке приводит к тому, что в кристалле распространяются упругие волны.

Упругие волны в кристалле имеют квантовые свойства, проявляющиеся в том, что существует наименьшая порция – квант энергии волны с данной частотой n. Это позволяет звуковой волне с частотой n сопоставить квазичастицу фонóн, который распространяется в кристалле со скоростью звука. Фонон обладает энергией E = hn.

Квазичастицы, в частности фононы, сильно отличаются от обычных частиц (например, электронов, протонов, фотонов), так как они связаны с коллективным движением многих частиц системы. Квазичастицы не могут возникать в вакууме, они существуют только в кристалле. Импульс фонона обладает своеобразным свойством: при столкновении фононов в кристалле их импульс может дискретными порциями передаваться кристаллической решетке – он при этом не сохраняется. Поэтому в случае фононов говорят о квазиимпульсе.

Энергия кристаллической решетки рассматривается как энергия фононного газа, подчиняющегося статистике Бозе-Эйнштейна, так как фононы являются бозонами (их спин равен нулю). Фононы могут испускаться и поглощаться, но их число не сохраняется постоянным. Поэтому химический потенциал фононного газа равен нулю.

При вычислении внутренней энергии кристалла и его теплоёмкости вводится характеристическая температура Дебая:

,

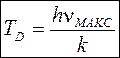где 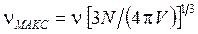– верхняя граница частот фононов, вносящих вклад в энергию тепловых колебаний кристалла (максимальная частота колебаний кристаллической решетки). При расчетах рассматривают два предельных случая:

а) при высоких температурах (T >> T_D) в результате вычислений получается закон Дюлонга и Пти: С = 3R;

б) при низких температурах (T << T_D) получается закон Дебая, из которого следует, что молярная теплоёмкость пропорциональна кубу температуры:

.
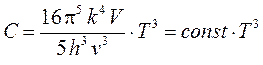