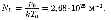|
|
Уравнение состояния идеального газа.
Как уже указывалось, состояние некоторой массы газа определяется тремя термодинамическими параметрами:
давлением р, объемом V и температурой Т. Между этими параметрами существует определенная связь, называемая уравнением состояния, котороев общем виде задается выражением

где каждая из переменных является функцией двух других.
Французский физик и инженер Б. Клапейрон (1799 — 1864) вывел уравнение состояния идеального газа, объединив законы Бойля — Мариотта и Гей-Люссака. Пусть некоторая масса газа занимает объем Vb имеет давление р1 и находится при температуре Тх. Эта же масса газа в другом произвольном состоянии характеризуется параметрами 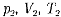
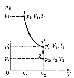
Переход из состояния 1 в состояние 2 осуществляется в виде двух процессов:
1) изотермического (изотерма 1—1'),
2) изохорного (изохора 1'—2).
В соответствии с законами Бойля —Мариотта (41.1) и Гей-Люссака (41.5)запишем: 
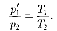
Исключив из уравнений (42.1) и(42.2) р[, получим 
Так как состояния 1 и 2 были выбраны произвольно, то для данной массы газа величина  остается постоянной, т.е.
остается постоянной, т.е. 
ыражение (42.3) является уравнением Клапейрона, в котором В — газовая постоянная, различная для разных газов.
Русский ученый Д.И.Менделеев(1834—1907) объединил уравнение Клапейрона с законом Авогадро, отнеся уравнение (42.3) к 1 моль газа, использовав молярный объем Vnv Согласно закону Авогадро, при одинаковых ри Т молярные объемы Vm различныхгазов одинаковы, поэтому постоянная В будет одинаковой для всех газов. Эта общая для всех газов постоянная обозначается R и называется молярной газовой постоянной. Уравнению 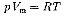
удовлетворяет лишь идеальный газ, и оно является уравнением состояния идеального газа, называемым также уравнением Клапейрона—Менделеева.
Числовое значение молярной газовой постоянной определим из формулы (42.4), полагая, что 1 моль газа находится при нормальных условиях (р0 = 1,013 • 105 Па, То = 273,15 К, VIU = 22,41 * 10~3 м3/моль):
R - 8,31 ДжДмоль • К). От уравнения (42.4) для 1 моль газа можно перейти к уравнению Клапейрона—Менделеева для произвольноймассы газа. Если при некоторых заданных давлении и температуре 1 моль газа занимает молярный объем Vm, то при тех же условиях масса т газа займет
объем  где М— молярная масса (масса 1 моль вещества). Единица молярной массы — килограмм на моль(кг/моль). Уравнение Клапейрона —Менделеева для массы т газа
где М— молярная масса (масса 1 моль вещества). Единица молярной массы — килограмм на моль(кг/моль). Уравнение Клапейрона —Менделеева для массы т газа  где
где  — количество вещества.
— количество вещества.
Часто пользуются несколько иной формой записи уравнения состояния идеального газа, вводя постоянную Больцмана:  Исходя из этого уравнение состояния (42.4) запишем ввиде
Исходя из этого уравнение состояния (42.4) запишем ввиде 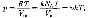 где
где  = п — концентрация молекул(число молекул вединице объема).
= п — концентрация молекул(число молекул вединице объема).
Таким образом, из уравнения р = пкТ (42.6)
следует, что давление идеального газа при данной температуре пропорционально концентрации его молекул (или плотности газа). При одинаковых температуре и давлении все газы содержат в единице объема одинаковое число молекул. Число молекул, содержащих-
ся в 1 м3 газа при нормальных условиях, называется числом Лошмидта1: