Главная | Обратная связь

Первое начало термодинамики.

Допустим, что некоторая система (газ, заключенный в цилиндр под поршнем), обладая внутренней энергией U₁, получила некоторое количество теплоты Q и, перейдя в новое состояние, характеризующееся внутренней энергией U₂, совершила работу А над внешней средой, т. е. против внешних сил. Количество теплоты считается положительным, когда оно подводится к системе, а работа — положительной, когда система совершает ее против внешних сил. Опыт показывает, что в соответствии с законом сохранения энергии при любом способе перехода системы из первого состояния во второе изменение внутренней энергии DU=U₂–U₁ будет одинаковым и равным разности между количеством теплоты Q, полученным системой, и работой А, совершенной системой против внешних сил:

Или

(51.1)

Уравнение (51.1) выражаетпервое начало термодинамики: теплота, сообщаемая систе­ме, расходуется на изменение ее внутренней энергии и на совершение ею работы против внешних сил. Выражение (51.1) в дифференциальной форме будет иметь вид

или в более корректной форме

(51.2)

где dU — бесконечно малое изменение внутренней энергии системы, dA — элементар­ная работа, dQ — бесконечно малое количество теплоты. В этом выражении dU является полным дифференциалом, а dA и dQ таковыми не являются. В дальнейшем будем использовать запись первого начала термодинамики в форме (51.2).

Из формулы (51.1) следует, что в СИ количество теплоты выражается в тех же единицах, что работа и энергия, т. е. в джоулях (Дж).

Если система периодически возвращается в первоначальное состояние, то измене­ние ее внутренней энергии DU=0. Тогда, согласно первому началу термодинамики,

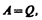
т. е. вечный двигатель первого рода — периодически действующий двигатель, который совершал бы бóльшую работу, чем сообщенная ему извне энергия, — невозможен (одна из формулировок первого начала термодинамики).

Работа газа при изменении его объема

Для рассмотрения конкретных процессов найдем в общем виде внешнюю работу, совершаемую газом при изменении его объема. Рассмотрим, например, газ, находя­щийся под поршнем в цилиндрическом сосуде (рис. 78). Если газ, расширяясь, пере­двигает поршень на бесконечно малое расстояние dl, то производит над ним работу

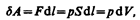
где S — площадь поршня, Sdl=dV— изменение объема системы. Таким образом, (52.1)

Полную работу А, совершаемую газом при изменении его объема от V₁ до V₂, найдем интегрированием формулы (52.1): (52.2)

Результат интегрирования определяется характером зависимости между давлением и объемом газа. Найденное для работы выражение (52.2) справедливо при любых изменениях объема твердых, жидких и газообразных тел.

Произведенную при том или ином процессе работу можно изобразить графически с помощью кривой в координатах р, V. Пусть изменение давления газа при его расширении изображается кривой на рис. 79. При увеличении объема на dV соверша­емая газом работа равна pdV, т. е. определяется площадью полоски с основанием dV, заштрихованной на рисунке. Поэтому полная работа, совершаемая газом при расшире­нии от объема V₁ до объема V₂, определяется площадью, ограниченной осью абсцисс, кривой p=f(V) и прямыми V₁ и V₂.

Графически можно изображать только равновесные процессы — процессы, состо­ящие из последовательности равновесных состояний. Они протекают так, что измене­ние термодинамических параметров за конечный промежуток времени бесконечно мало. Все реальные процессы неравновесны (они протекают с конечной скоростью), но в ряде случаев неравновесностью реальных процессов можно пренебречь (чем медлен­нее процесс протекает, тем он ближе к равновесному). В дальнейшем рассматриваемые процессы будем считать равновесными.