 |
|
Распределение Максвелла.
Молекулы газа совершают хаотическое движение. В результате многократных соударений скорость каждой молеулы изменяется как по модулю, так и по направлению. Однако из-за хаотического движения молекул все направления движения являются равновероятными, т.е. в любом направлении в среднем движется одинаковое число
молекул. По молекулярно-кинетической теории, как бы ни изменялись скорости молекул при столкновениях, средняя квадратичная скорость молекул массой т 0 в газе, находящемся в состоянии равновесия при ( Т= const), остается постоянной и равной(vKn) — 
Закон Максвелла описывается некоторой функциейf(v),называемой функцией распределения молекул по ско-
ростям. Если разбить диапазон скоростей молекул на малые интервалы, равные dv, то на каждый интервал скорос- 
ти будет приходиться некоторое число молекул dN(v), имеющих скорость, заключенную в этом интервале. Функция
f(v) определяет относительное число (долю) молекул 
, скорости которых лежат в интервале от v до v + dv, т. е. 
откуда 
Применяя методы теории вероятностей, Максвелл нашел функцию f(v) —закон распределения молекул идеального газа по скоростям: 
Из (44.1) видно, что конкретный вид функции зависит от рода газа (от массы молекулы) и от параметра состояния
(от температуры Т). График функции (44.1) приведен на
рис. 67. Так как при возрастании v мно-
чем растет множитель v2, то функция f(v), начинаясь от нуля, достигает максимума при vK изатем асимптотически
стремится кнулю. Кривая несимметрична относительно v.
Относительное число молекул 
скорости которых лежат в интервале от v до v + dv, находится как площадь тонированной полоски на рис. 67. Смысл
этого интеграла в следующем: если просуммировать все доли молекул, имеющих всевозможные значения скоростей,
то получим единицу. Функция f(v)удовлетворяет условию нормировки 
Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется
наиболее вероятной скоростью. Значение наиболее вероятной скорости можно найти, продифференцировав
выражение (44.1) (постоянные множители опускаем) по аргументу v, приравняв результат нулю и используя усло-
вие для максимума выражения f(v) 
:Значения v = 0 и v = ос соответствуют минимумам выражения (44.1), a
значение v, при котором выражение в скобках становится равным нулю, и есть искомая наиболее вероятная ско-
рость v: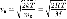 
Из формулы (44.2) следует, что при повышении температуры максимум функции распределения молекул по скоростям (рис. 68) сместится вправо (значение наиболее вероятной скорости становится больше). Однако площадь, ограниченная кривой, остается неизменной, поэтому при повышении температуры кривая распределения
молекул по скоростям будет растягиваться и понижаться.
Средняя скорость молекулы (v) (средняя арифметическая скорость)определяется по формуле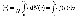 
Подставляя сюда f(v) иинтегрируя, получим 
Скорости, характеризующие состояние газа: 1) наиболее вероятная 
= l,13vB; 3) средняя квадратичнаяИсходя из распределения молекул по ско-
ростям 
можно найти распределение молекулгаза по значениям кинетической энер-
гии е. Для этого перейдем от переменной v к переменной 
Подставив в (44.4) v и 
получим 
где diV(e) — число молекул, имеющих
кинетическую энергию поступательного движения, заключенную в интервале от £ до е + de.
Таким образом, функция распределения молекул по энергиям теплового движения 
Средняя кинетическая энергия (е)молекулы идеального газа 