 |
|
Возрастание и убывание функций.
Сидоренкова И.В.
Приложения производной к исследованию функций
И построение графиков
Учебное пособие
Королев, 2008
Сидоренкова И.В. Приложения производной к исследованию функций и построение графиков. – Королев: КИУЭС, 2008, 18 с.
Рецензент:д. ф. – м. н., профессор Борисов В. Ф.
Учебное пособие предназначено для проведения практических занятий и для самостоятельной работы студентов по курсу Математический анализ, раздел “Применение производных к построению графиков функций”. Содержание раздела соответствует требованиям Государственных образовательных стандартов высшего профессионального образования и Учебным планам КИУЭС для всех специальностей.
| РЕКОМЕНДОВАНО Учебно-методическим советом КИУЭС Протокол № 8 от 15.05.2007 г. | Учебное пособие рассмотрено и одобрено на заседании кафедры математики. Протокол № 7 от 4.4.2007 г. |
| Зав. кафедрой математики д. ф. – м. н., профессор Борисов В.Ф. |
Введение.
Изучение количественной стороны различных явлений природы приводит к установлению и изучению функциональной зависимости между участвующими в данном явлении переменными величинами. Если такую зависимость можно выразить аналитически, т. е. в виде одной или нескольких формул, то мы получаем возможность исследовать эту функциональную зависимость средствами математического анализа. Нашей целью является установление общих приёмов исследования поведения функций. Применение дифференциального исчисления к исследованию функций опирается на весьма простую связь, существующую между поведением функции и свойствами её производных, прежде всего её первой производной.
Возрастание и убывание функций.
Пусть функция f(x) определена и непрерывна на отрезке [a,b]. Если для любых x1, x2 
[a, b]таких, что x1 < x2 
f(x1) < f(x2) (меньшему значению аргумента соответствует меньшее значение функции), то функция f(x) называется возрастающей на отрезке [a,b] (рис. 1).
Аналогично, функция f(x) называется убывающей на отрезке [a,b], если для любых x1, x2 [a, b]таких, что x1 < x2 f(x1) > f(x2) (большему значению аргумента соответствует меньшее значение функции) (рис. 2).
f(x2) f(x1)
f(x1) f(x2)
0 a x1 x2 b 0 a x1 x2 b
Рис. 1 Рис. 2
Как интервал возрастания, так и интервал убывания функции называют интервалами монотонности функции, а функцию на этом интервале – монотонной функцией.
Обычно интервал, на котором рассматривается функция, можно разбить на ряд интервалов, в каждом из которых функция монотонна (см. рис. 3).
Y
x1 x2 x3 X
Рис. 3
Теорема (достаточный признак монотонности).
Пусть функция f(x) непрерывна на отрезке [a,b] и дифференцируема во всех его внутренних точках. Тогда если 
> 0 для всех x (a,b) , то функция f(x) возрастает на [a,b]. Если < 0 для всех x (a,b), то функция f(x) убывает на [a,b].
Доказательство основано на формуле конечных приращений Лагранжа. В самом деле, согласно формуле Лагранжа, для любых x1, x2 (a,b)таких, что x1 < x2имеем f(x2) - f(x1) = 
(x2 – x1), x1 < ξ < x2. Т. к. x1 < x2, то x2 – x1 > 0 и знак разности f(x2)-f(x1) полностью определяется знаком производной . Если >0, то f(x2) - f(x1) > 0 и f(x2) >f(x1), т. е. функция f(x) возрастает на [a,b].
Аналогично доказывается: если < 0 для всех x (a,b) , то функция f(x) убывает на [a,b] .
Эта теорема даёт нам простой и удобный признак монотонности функции на интервале.
Пример. Исследовать функцию y=(х – 3) 
на убывание и возрастание.
Решение.Находим производную для х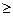 
0:
+(x – 3) 
= 
.
При х = 1 имеем 
= 0. Если х (0,1), то < 0 на этом интервале функция у(х) убывает; если х (1, 
), 
то > 0 на интервале (1, ) функция у(х) возрастает.
Задание. Исследовать на возрастание и убывание следующие функции:
y = 
; 
y = x – 
y = 