 |
|
Общая схема исследования функции.
1.а) Найти область определения функции .
б) Найти точки разрыва функции и интервалы непрерывности.
в) Исследовать поведение функции в окрестностях точек разрыва; найти вертикальные асимптоты.
г) Найти точки пересечения графика с осями координат, интервалы знакопостоянства функции.
д) Исследовать функцию на чётность, нечётность, периодичность.
2.Установить интервалы монотонности функции, найти точки экстремума и экстремальные значения.
3.Установить интервалы выпуклости и вогнутости функции; найти точки перегиба.
4. Исследовать поведение функции в бесконечности. Найти наклонные (в частности, горизонтальные ) асимптоты.
5.Построить график функции.
Замечания.
1.Выполнение 4–го раздела иногда удобно производить вместе с первым, когда выясняется общая картина поведения функции.
2.Выполнение всех разделов следует сопровождать постепенным построением графика функции. При этом, прежде всего, нужно на оси ОХ выделить характерные точки, к которым относятся: точки разрыва, нули, точки экстремума, абсциссы точек перегиба. На плоскости ОХУ отмечаются точки графика, соответствующие этим выделенным значениям аргумента.
Пример 1.
Построить график функции у = (х + 5) 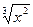 .
.
Решение.
Область определения функции (–  ,+
,+  ). Функция непрерывна на всей числовой оси, точек разрыва нет.
). Функция непрерывна на всей числовой оси, точек разрыва нет.
Вертикальных асимптот нет; k1,2 = 
 =
= 
 =
=  , наклонных асимптот нет.
, наклонных асимптот нет.
Функция не является ни чётной, ни нечётной, ни периодической.
 (х) =
(х) =  .
.  (х) = 0 при х = –2,
(х) = 0 при х = –2,  (х) не существует при х = 0.
(х) не существует при х = 0.
| х | (–  ,–2) ,–2)
| –2 | (–2,0) | (0,+  ) )
| |
Знак  (х) (х)
| + |  = 0 = 0
| – |  = + = + 
| + |
| Поведение функции | Возрастает | max
3 
| Убывает | min | Возрастает |
 =
= 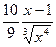 ;
;  = 0 при х = 1,
= 0 при х = 1,  не существует при х = 0.
не существует при х = 0.
| х | (–  ,0) ,0)
| (0,1) | (1,+  ) )
| ||
Знак 
| – |  = – = – 
| – |  = 0 = 0
| + |
| Поведение функции | Выпукла | Не является точкой перегиба | Выпукла | Точка перегиба у = 6 | Вогнута |
у( х)= 0 при х = 0 и х = –5.
Строим график функции (рис.13 ).


Рис. 13
Пример 2.
Построить график функции у =  .
.
Решение.
Область определения функции – любое число, кроме х = 1 и х =–1. Для значений х > 1 и –1 < х < 0 функция отрицательна, для значений х < –1 и 0 < х < 1 – положительна. Функция непрерывна на (–  ,–1), (–1,1), (1,+
,–1), (–1,1), (1,+  ).
).
Т. к.  у(x)=–
у(x)=–  ,
,  у(x)=+
у(x)=+  ,
,  у(x)=+
у(x)=+  ,
,  у(x)=–
у(x)=–  , то прямые х = 1 и х = –1 – вертикальные асимптоты.
, то прямые х = 1 и х = –1 – вертикальные асимптоты.
 (х) =
(х) =  , х
, х  –1,1.
–1,1.
 (х) = 0 при х1 = 0 , х2 =
(х) = 0 при х1 = 0 , х2 =  , х3= –
, х3= –  .
.
| х | (–  ,– ,–  ) )
| – 
| (–  , –1) , –1)
| –1 | (–1,0) |
Знак  (х) (х)
| – | + | + | ||
| Поведение функции | Убывает | min | Возрастает | Возрастает |
| (0,1) | (1,  ) )
| 
| (  ,+¥) ,+¥)
| ||
| + | + | – | |||
| Нет extr | Возрастает | Возрастает | max | Убывает |
В точках х = 1 и х = -1 производная  (х) не существует, они не являются точками экстремума, т.к. в них функция терпит разрыв.
(х) не существует, они не являются точками экстремума, т.к. в них функция терпит разрыв.
Находим вторую производную:  =
=  , х
, х  –1,1. Исследуем её знаки:
–1,1. Исследуем её знаки:
| х | (–  ,–1) ,–1)
| –1 | (–1,0) | (0, 1) | (1,+  ) )
| ||
Знак 
| + | не сущ. | – | + | не сущ. | – | |
| Поведение функции | Вогнута | Выпукла | Точка перегиба | Вогнута | Выпукла | ||
Поскольку k1,2 = 
 =
= 
 = –1; b1,2 =
= –1; b1,2 =  ( f(x) - k1x ) =
( f(x) - k1x ) =
= 
 = 0, то у = –х правая и левая асимптоты.
= 0, то у = –х правая и левая асимптоты.
Строим график (рис. 14 ).





Рис. 14
Пример 3.Построить график функции у =  .
.
Решение.Функция определена для всех х, кроме х = 0. Для значений х > 0 функция положительна, а для значений х < 0 отрицательна.
Функция непрерывна всюду, кроме точки х = 0, причём 
 = +
= +  ,
, 
 = –
= –  . Следовательно, прямая х= 0 является вертикальной асимптотой.
. Следовательно, прямая х= 0 является вертикальной асимптотой.
Для всех х, отличных от х = 0, имеем  (х) =
(х) = 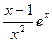 .
.  (х) = 0 в точке х = 1. На интервалах (–
(х) = 0 в точке х = 1. На интервалах (–  ,0) и (0,1) производная
,0) и (0,1) производная  (х) > 0 и, следовательно, функция возрастает. Точка х=1 является точкой локального минимума, причём у(1) = е.
(х) > 0 и, следовательно, функция возрастает. Точка х=1 является точкой локального минимума, причём у(1) = е.
 =
=  .
.
Выражение х2 – 2х + 2 = ( х – 1)2 + 1 > 0 для любых х, поэтому на интервале (-  ,0)
,0)  < 0, а на интервале (0,+
< 0, а на интервале (0,+  )
)  > 0, следовательно, на интервале (-
> 0, следовательно, на интервале (-  ,0) функция выпукла, а на интервале (0,+
,0) функция выпукла, а на интервале (0,+  ) –вогнута. Точек перегиба нет.
) –вогнута. Точек перегиба нет.
Найдем наклонные асимптоты:
k1 = 
 =
= 
 = +
= +  , k2=
, k2= 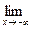
 =
= 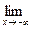
 = 0, b2 =
= 0, b2 = 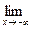
 = 0.
= 0.
Следовательно, у =0 – горизонтальная асимптота при х  .
.
Пользуясь результатами исследования, строим график (рис. 15 ).

Рис. 15
Пример 4.Исследуем функцию у =  .
.
1.Функция определена и непрерывна на всей оси ОХ. Т. к. у > 0 при всех х, то график целиком лежит над осью абсцисс. Функция чётная; значит, график симметричен относительно оси ОУ. При х →  ∞ функция стремится к 0, поэтому ось абсцисс является горизонтальной асимптотой.
∞ функция стремится к 0, поэтому ось абсцисс является горизонтальной асимптотой.
2. 
 .
.
В интервале (–  ,0)
,0)  (х) > 0
(х) > 0  функция возрастает.
функция возрастает.
В интервале (0, +  )
)  (х) < 0
(х) < 0  функция убывает.
функция убывает.
В точке х = 0 – максимум ; у(0) = 1, и это значение является наибольшим значением функции.
По найденным данным уже можно схематически строить график функции. При его построении станет ясно, что имеются точки перегиба; найдём их.
3.  =
=  ∙ (х2 – 1).
∙ (х2 – 1).
Корнями уравнения  = 0 служат точки х = 1 и х =–1. Знак второй производной зависит только от знака второго множителя: он положительный в интервалах (–
= 0 служат точки х = 1 и х =–1. Знак второй производной зависит только от знака второго множителя: он положительный в интервалах (–  ,–1) и (1,+
,–1) и (1,+  ) и отрицательный в интервале (–1,1). Значит, в двух крайних интервалах график функции вогнутый, а в среднем интервале – выпуклый. Значение функции в точках перегиба равно
) и отрицательный в интервале (–1,1). Значит, в двух крайних интервалах график функции вогнутый, а в среднем интервале – выпуклый. Значение функции в точках перегиба равно
у (–1) = у (1) = 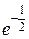
 0,6065.
0,6065.
Строим график функции (рис. 16). Исследуемая функция очень часто встречается при изучении теории вероятностей.

Рис. 16
Литература
1. Щипачев В.С. Высшая математика. Учебник для вузов. Высшая школа, 2001.
2. Кремер Н.Ш. Высшая математика для экономистов. Учебник. 2 издание. Юнити – Дана, 2002.
Содержание
| № | Раздел | Стр. |
| Введение | ||
| Возрастание и убывание функций. | ||
| Экстремумы функции. | ||
| Необходимый признак экстремума. | ||
| Правило нахождения экстремума. | ||
| Исследование кривых на выпуклость и перегиб. | ||
| Достаточное условие выпуклости. | ||
| Исследование кривых на перегиб. | ||
| Асимптоты. | ||
| Общая схема исследования функции. | ||
| Литература | ||
| Содержание |