 |
|
Правило нахождения экстремума.
 1. Продифференцировать функцию.
1. Продифференцировать функцию.
 2. Найти точки, в которых производная обращается в 0: в этих точках возможен экстремум.
2. Найти точки, в которых производная обращается в 0: в этих точках возможен экстремум.
 3. Выяснить знак производной в окрестности критической точки:
3. Выяснить знак производной в окрестности критической точки:
если слева от точки производная положительна, а справа отрицательна, то функция в этой точке имеет максимум (рис. 7);если слева от точки производная функции отрицательна, а справа положительна, то функция в этой точке имеет минимум (рис. 8).
 Если справа и слева от точки функция имеет один и тот же знак, то функция в этой точке экстремума не имеет.
Если справа и слева от точки функция имеет один и тот же знак, то функция в этой точке экстремума не имеет.

 Y Y
Y Y
 f´(x)=0
f´(x)=0
 |  | ||
f´(x)>0 f´(x)<0
 f´(x) <0
f´(x) <0
f´(x)>0
 f´(x)=0
f´(x)=0
 |  |
0 X 0 X
Рис. 7 Рис. 8
Правило поясняется таблицей 1(здесь х1 < х0< х2).
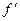 (x0) (x0)
| 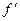 (x1) (x1)
| 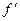 (x2) (x2)
| f(x0) |
| + | – | max | |
| – | + | min | |
| + | + | extr нет | |
| – | – | extr нет |
Пример. Исследовать на экстремум функцию y=2x3 – 3x2.
Решение. Дифференцируем функцию:  = 6x2 – 6x. Находим точки, в которых производная обращается в 0,т.е. находим корни уравнения 6x2 – 6x = 0,
= 6x2 – 6x. Находим точки, в которых производная обращается в 0,т.е. находим корни уравнения 6x2 – 6x = 0,
6x ( x – 1) = 0, х1 = 0, х2 = 1.
Экстремум возможен только в этих точках. Находим знак производной слева и справа от точки х1= 0:
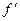 (–1) = 6·(–1) 2 – 6·(–1) = 12 > 0,
(–1) = 6·(–1) 2 – 6·(–1) = 12 > 0,
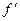 (
(  ) = 6·(
) = 6·(  ) 2 – 6·
) 2 – 6·  = –
= –  < 0.
< 0.
В точке х1 = 0 функция y= 2x3– 3x2имеет максимум.
Находим знак производной слева и справа от точки х2 = 1:
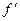 (
(  ) = –
) = –  < 0,
< 0,
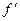 (2) = 6·22 – 6·2 = 12 > 0.
(2) = 6·22 – 6·2 = 12 > 0.
В точке x2 = 1функция имеет минимум.
Т. к. в точке экстремума функция переходит от возрастания к убыванию и наоборот, то можно указать интервалы возрастания и убывания функции: на интервале (–  ;0) функция возрастает, на интервале (0,1) – убывает, на интервале (1,+
;0) функция возрастает, на интервале (0,1) – убывает, на интервале (1,+  ) – возрастает.
) – возрастает.
Задания. Исследовать следующие функции на возрастание, убывание и точки экстремума:
у ( х) = 3х2 + 5; у( х) = 1 – 7х2; у( х) =  –
– 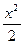 – 2х;
– 2х;
у(х) =  ; у(х) =
; у(х) =  ; у(х) = х –
; у(х) = х –  ; у(х) = х ·e-x; у(х) = x + ex;
; у(х) = х ·e-x; у(х) = x + ex;
у(х) =  +
+  ; у( х) = х ln x.
; у( х) = х ln x.
Исследование кривых на выпуклость и перегиб.
Определение 1.
Функцию у = f(x) называют выпуклой на промежутке I=[a,b], если
f((1 – λ)·x1 + λ·x2 ) < (1 – λ)·f(x1) + λ·f(x2)
для всех λ 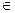 (0,1) и всех x1 , x2
(0,1) и всех x1 , x2 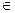 I таких, что x1 < x2 .
I таких, что x1 < x2 .
Выпуклость функции имеет простой геометрический смысл:
функция у = f(x), заданная на промежутке I, выпукла тогда и только тогда, когда всякая дуга её графика лежит над стягивающей её хордой (рис. 9).
Определение 2.Функцию у = f(x) называют вогнутой на промежутке I, если функция – f(x) выпукла на I.
Сравнивая с определением 1, видим, что функция у = f(x) вогнута на промежутке I тогда и только тогда, когда для всех λ 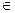 (0,1) и всех x1 , x2
(0,1) и всех x1 , x2 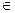 I таких, что x1 < x2 , выполняется неравенство
I таких, что x1 < x2 , выполняется неравенство
f((1 – λ)·x1 + λ·x2 )> (1 – λ)· f(x1) + λ· f(x2).
Вогнутость функции у = f(x) на промежутке I означает, что всякая дуга её графика лежит под хордой, стягивающей эту дугу (рис. 10).

 Y Y
Y Y
 | |||
 |
O x1 x2 X O x1 x2 X
Рис. 9 Рис. 10