Главная | Обратная связь

Достаточное условие выпуклости.

Пусть функция y=f(x) определена и дважды дифференцируема на интервале (а,b). Тогда:

а) если (x) < 0 для любого х (а,b) , то функция y=f(x) выпукла на этом интервале;

б) если (x) > 0 для любого х (а,b) , то функция y=f(x) вогнута на этом интервале.

Определение. Пусть y=f(x) – дифференцируемая функция на промежутке I. Точка х₀ 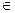I называется точкой перегиба функции y=f(x), если при переходе через неё функция меняет выпуклость на вогнутость или наоборот.

Точку М(х₀,f(x₀)) называют точкой перегиба графика функции y=f(x).

Замечание.Касательная пересекает кривую в точке перегиба (рис.11).

Y

 

 

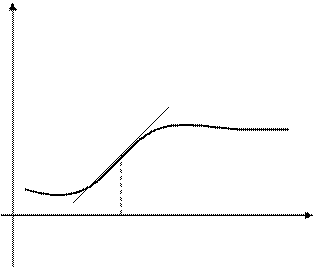
0 x₀X

 

Рис. 11

В точке перегиба х₀ дважды дифференцируемой функции y=f(x)её вторая производная обращается в 0: (x₀) = 0 (необходимый признак точек перегиба). Если при переходе через точку х₀ вторая производная (x) меняет знак, то x₀ является точкой перегиба (достаточный признак точек перегиба).

 

Исследование кривых на перегиб.

1. Для того, чтобы кривая y=f(x) имела перегиб при х = х₀, необходимо, чтобы ( x₀) = 0.

2. Для того, чтобы кривая y=f(x) имела перегиб при х = х₀, достаточно, чтобы слева и справа от точки x₀ функция (x) имела разные знаки.

Если (x) знак не меняет, то x₀ не является точкой перегиба.

Примеры.

1. Найти точки перегиба и интервалы выпуклости функции у(х) = х³ .

Решение. 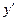(х) = 3х²; (х) = 6х.

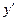(х) = 0 при х = 0, причём (0) = 0 (в точке х = 0 существует касательная к графику ).

(х) < 0 при х <0 и (х) > 0 при х > 0 точка х = 0 является точкой перегиба функции у( х) = х³.

2. Найти точки перегиба и интервалы выпуклости функции у( х) = (1 + х²) е^х.

Решение.

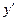(х) = 2х е^х + (1 + х²) е^х = е^х (1 + х)².

(х) = е^х (1 + х)² + 2 е^х (1 + х) = е^х (1 + х)(3 + х).

(х) = 0, если х₁ = –3, х₂ = –1.

Следовательно, в точках х₁ = –3, х₂ = –1 функция имеет перегиб, т.к. (х) меняет знак, проходя через эти точки; на интервалах (– , –3) и (–1, + ) функция выпукла вниз, на интервале (–3, –1) функция выпукла вверх.

Задания. Исследовать следующие функции на выпуклость и точки перегиба: у ( х) = 1 – х ³ ; у ( х) = х ³ – 3х; у ( х) = х ³ – х²; у( х) = е^х + е ^–х;;

у( х) = х – ln x; у( х) = х² ln x; у( х) = ln² х.

 

Асимптоты.

Когда мы хотим изучить функцию при стремлении аргумента к бесконечности, нам приходится иметь дело с частями графика, уходящими в бесконечность, так называемыми бесконечными ветвями графика. С бесконечными же ветвями нам приходится иметь дело и тогда, когда мы рассматриваем функцию вблизи точек её бесконечного разрыва.

Знание бесконечных ветвей функции необходимо для того, чтобы правильно представить себе форму всего графика и, следовательно, характер изменения функции во всей области её определения.

Подойдём к вопросу с геометрической точки зрения и введём определение асимптоты линии.

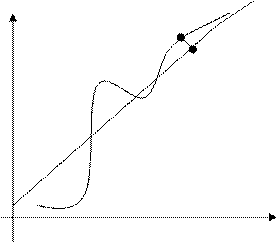
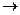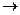Определение.Прямая у = kx + b есть асимптота графика функции y=f(x)при (х – ) , если расстояние от точки М(х,f(x)) графика до этой прямой стремится к 0 при (х – ) (рис.12) .

Y Y у = kx + b

 

y=f(x) М(х,f(x))

у = kx + b

y=f(x)

М(х,f(x))

 

O X O X

Рис. 12

Следует различать случаи вертикальной и наклонной асимптот.

1). Пусть график функции y=f(x) имеет вертикальную асимптоту. Уравнение такой асимптоты будет х = х₀, а поэтому, согласно определению асимптоты, f(x) → ∞ при х → х_0.

Итак, прямая х = х₀ будет вертикальной асимптотой графика функции y=f(x) , если хотя бы один из пределов равен + или – .

Если существует конечный предел = k₁ и (f(x) – k₁x) = b₁, то прямая у = k₁x + b₁ будет правой асимптотой графика функции y=f(x) при ( при k₁ = 0 асимптота будет горизонтальной ).

Если существует конечный предел 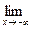= k₂ и 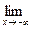( f(x) – k₂x ) = b₂, то прямая у = k₂ x + b₂ будет левой асимптотой графика функции y=f(x) при х 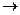- (при k₂ = 0 асимптота будет горизонтальной ).

Если хотя бы один из этих пределов не существует или бесконечен, то соответствующей асимптоты нет.