Главная | Обратная связь

Необходимый признак экстремума.

Если в точке х₀ функции у = f(x) достигает локального экстремума, то её производная в этой точке равна 0 (этот признак является следствием теоремы Ферма).

С геометрической точки зрения это означает, что касательная к графику функции в точке локального экстремума параллельна оси ОХ (рис.5).

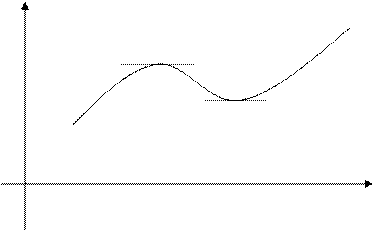Y

 

max

 

 

min

 

0 X

Рис.5

Замечание.Функция может иметь экстремум и в тех точках, в которых она недифференцируема.

Пример.у = . В точке х = 0 производная функции не существует , однако х = 0 является точкой минимума (рис.6).

Рис.6

Необходимый признак экстремума не является достаточным, т. е. из того, что производная в данной точке обращается в 0, ещё не следует, что эта точка обязательно будет точкой локального экстремума.

Пример.Производная функции у=х³ в точке х₀ = 0 равна 0:

= 3х², (0) = 0.

Однако, точка х₀не является точкой экстремума, т.к. справа от неё значения функции отрицательны, а слева положительны.

 

Теорема (достаточный признак экстремума).

Пусть функция у = f(x) непрерывна и некоторой окрестности точки х₀и имеет в ней производную всюду, кроме, быть может, самой точки х₀. Тогда: если слева от точки х₀производная функции положительна, а справа отрицательна, то х₀ есть точка локального max функции у = f(x);

если справа от точки х₀производная функции отрицательна, а слева положительна, то х₀ есть точка локального min функции у = f(x).

Если при переходе через точку х₀ производная знака не меняет, то экстремума в этой точке не будет.

 

Укажем последовательность действий для отыскания точек экстремума и интервалов монотонности функции. Пусть функция у = f(x) в заданном интервале (конечном или бесконечном) непрерывна и имеет производную всюду, за исключением, быть может, отдельных точек. Будем для простоты считать, что если эти отдельные точки исключить, то в оставшихся интервалах производная тоже непрерывна.