 |
|
Понятие линейной зависимости векторов.
Определение 9.Пусть дана система векторов 
1, 2, …, n и совокупность 
вещественных чисел 
. Тогда выражение вида 
называется линейной комбинацией векторов, а числа называются коэффициентами линейной комбинации. Если некоторый вектор представлен как линейная комбинация векторов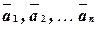 
, т.е. в виде: 
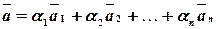, то говорят, что вектор разложен по этим векторам.
Определение 10.Векторы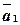 
, 
, …, 
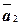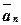называются линейно зависимыми, если существует набор коэффициентов , одновременно не равных нулю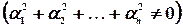 
и таких, что
.
Определение 11.Векторы 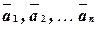называются линейно независимыми, если равенство нулю линейной комбинации этих векторов возможно лишь при всех коэффициентах одновременно равных нулю.
Определение 12. Базисом на прямой называется любой ненулевой вектор на этой прямой.
Определение 13. Базисом на плоскости называются два неколлинеарных вектора на этой плоскости, взятые в определенном порядке.
Определение 14.Базисом в пространстве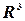 
называются три линейно независимые вектора в этом пространстве, взятые в определенном порядке.
Теорема 1 (о разложении вектора по базису в пространстве R3)
Пусть даны три некомпланарные вектора: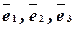 
. Любой вектор раскладывается по ним. Такое разложение единственно. Существует набор чисел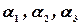 
такой, что:
.
Свойства линейно зависимой и линейно независимой системы векторов:
1) Если хотя бы один из векторов есть нуль вектор, то все векторов линейно зависимы.
2) Если среди векторов какие-либо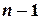 
векторов линейно зависимы, то все векторов линейно зависимы.
3) Для того чтобы два ненулевых вектора были линейно зависимы необходимо и достаточно, чтобы они были коллинеарными.
4) Пусть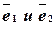 
- два неколлинеарных вектора плоскости. Любой компланарный с ними вектор раскладывается по ним: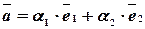 
. Такое разложение единственно.
5) Три компланарных вектора линейно зависимы. Три некомпланарных вектора пространства линейно независимы.
6) Любые четыре вектора пространства 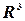линейно зависимы.
7) Система векторов 1, 2, …, n линейно зависима тогда и только тогда, когда один из них раскладывается в линейную комбинацию остальных.