 |
|
Свойства векторного произведения векторов.
1) Векторное произведение коллинеарных векторов равно нулю.
.
2) Антикоммутативность: 
.
3) Ассоциативность относительно скалярного множителя:
( 
).
4) Дистрибутивность: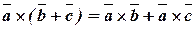 
.
Таблица векторного умножения ортонормированного базиса 
, 
, 
.
.
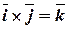
Для запоминания можно воспользоваться круговым правилом:
Если перемещаться последовательно от одного к другому вектору против хода часовой стрелки, то следующий вектор надо писать со знаком (+), а по ходу стрелки следующий вектор со знаком (-).
Пример 12. Даны точки 
, 
, 
, 
.
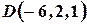Найти векторное произведение 
и его модуль.
Решение. Найдем
, 
,
, 
По формуле векторного произведения, имеем
.
Таким образом, векторное произведение имеет координаты:
, а его модуль
.
Пример 13. Даны точки , , .
Найти площадь треугольника 
.
Решение. Найдем , 
.
Векторное произведение 
и его модуль найдем как.
,
, 
.
Применив формулу площади для треугольника 
, построенного на векторах 
и 
, запишем 
. Отсюда получаем, что 
(кв. ед.).
Пример 14. Найти 
, если 
, 
, 
, 
.
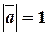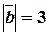Решение. Используя свойства векторного произведения, упростим конструкцию вектора 
, а именно:
.
Так как 
, то 
. Следовательно,
.
Теперь по формуле модуля векторного произведения, получаем
.
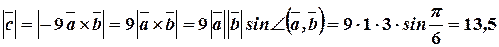Пример 15. Зная векторы 
и 
, вычислите длину высоты 
треугольника (см. рис).
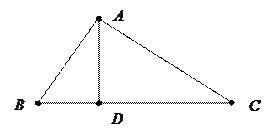Решение. Обозначая площадь треугольника через 
, получим:
. Тогда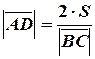 
, 
. С другой стороны, площадь треугольника определяется через векторное произведение как: 
.
Длину стороны найдем из равенства: 
. Значит, вектор имеет координаты 
.
.
Следовательно, модуль этого векторного произведения равен:
,
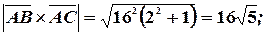
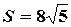Откуда
.
Пример 16. Даны два вектора 
и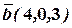 
. Найдите единичный вектор , ортогональный векторам 
и 
и направленный так, чтобы упорядоченная тройка векторов , , была правой.
Решение. Обозначим координаты вектора относительно данного правого ортонормированного базиса через 
.
Поскольку 
, и 
, то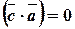
,
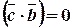. По условию задачи требуется, чтобы 
и 
.
Имеем систему уравнений для нахождения :
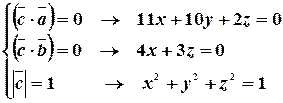
Из второго уравнения системы получим: 
. Подставим в первое
.
Подставляя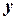 
и 
в третье уравнение, будем иметь: 
, откуда 
.
Используя условие , получим неравенство
Или
Отсюда
С учетом выражений для 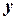и перепишем полученное неравенство в виде: 
, откуда следует, что 
. Итак, 
, 
, 
.