 |
|
Угол между двумя векторами.
Из определения скалярного произведения:
.
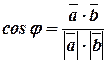
Условие ортогональности двух векторов:
Условие коллинеарности двух векторов:
.
Следует из определения 5 - 
. Действительно, из определения произведения вектора на число, следует 
. Поэтому, исходя из правила равенства векторов, запишем 
, 
, 
, откуда вытекает 
. Но вектор 
, получившийся в результате умножения вектора 
на число 
, коллинеарен вектору 
.
Проекция вектора на вектор:
.
Пример 4. Даны точки 
, 
, 
, 
.
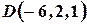Найти скалярное произведение 
.
Решение. 
найдем по формуле скалярного произведения векторов, заданных своими координатами. Поскольку
, 
,
, 
то 
.
Пример 5.Даны точки , , , .
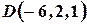Найти проекцию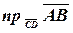 
.
Решение. Поскольку
, ,
,
то и 
.
На основании формулы проекции, имеем
.
Пример 6.Даны точки , , , .
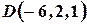Найти угол между векторами 
и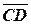 
.
Решение. Заметим, что вектора
, ,
,
не являются коллинеарными, поскольку не пропорциональны их координаты:
.
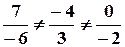Эти вектора не являются также перпендикулярными, так как их скалярное произведение 
.
Найдем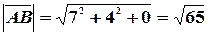 
,
Угол 
найдем из формулы:
.
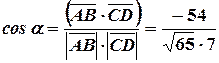Пример 7. Определить при каких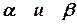 
вектора 
и 
коллинеарны. 
Решение. В случае коллинеарности, соответствующие координаты векторов 
и 
должны быть пропорциональны, то есть:
.
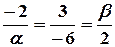Отсюда 
и 
.
Пример 8. Определить, при каком значении вектора 
и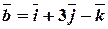 
перпендикулярны.
Решение. Вектора 
и 
перпендикулярны, если их скалярное произведение 
равно нулю. Из этого условия получаем: 
. Стало быть, 
.
Пример 9. Найти 
, если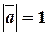 
, 
, 
.
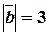Решение. В силу свойств скалярного произведения, имеем:
Пример 10. Найдите угол между векторами 
и 
, где 
и 
-единичные векторы и угол между векторами и равен 120о.
Решение. Имеем: 
, 
, 
Значит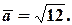 
Значит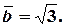 
Окончательно имеем: 
.
5.б. Векторное произведение.
Определение 21.Векторным произведением вектора на вектор называется вектор 
, или 
, определяемый следующими тремя условиями:
1) Модуль вектора 
равен 
, где 
- угол между векторами и , т.е. 
.
Отсюда следует, что модуль векторного произведения численно равен площади параллелограмма, построенного на векторах и как на сторонах.
2) Вектор перпендикулярен к каждому из векторов и ( 
; 
), т.е. перпендикулярен плоскости параллелограмма, построенного на векторах и .
3) Вектор направлен так, что если смотреть из его конца, то кратчайший поворот от вектора к вектору был бы против часовой стрелки (векторы , , образуют правую тройку).