 |
|
Дифракция Френеля на круглом отверстии
Рассмотрим пучок лучей, распространяющихся от точечного источника монохроматического света 
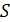(рис. 2.4). В этом случае волновой фронт 
в любой момент времени будет представлять собой сферу некоторого радиуса 
. Дифракцию со сферическим волновым фронтом называют дифракцией Френеля. Зоны Френеля на данной волновой поверхности мы получим, если из точки наблюдения 
, находящейся на расстоянии 
от волновой поверхности, проведем сферы радиусами, отличающимися друг от друга на половину длины световой волны. То есть радиусы этих сфер будут последовательно равны
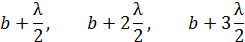
и т. д. Эти сферы разобьют волновой фронт на кольцевые зоны.
Эти кольцевые зоны и есть зоны Френеля, поскольку разность хода лучей от краев соседних зон до точки наблюдения равна половине длины волны (рис. 2.4).
Определим радиусы зон Френеля для данного случая. Рассмотрим рис. 2.5, где – волновая поверхность радиусом ; – расстояние от центра волновой поверхности до точки наблюдения ; 
– расстояние от 
-й зоны Френеля до точки наблюдения ; 
– радиус сферического сегмента, выделяемого на волновой поверхности границей -й зоны Френеля; 
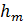– высота сферического сегмента.
|
| Рис. 2.5 |
|
|
|
|
|
|
|
|
|
|
|
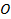
Запишем теорему Пифагора для двух прямоугольных треугольников с общим катетом :
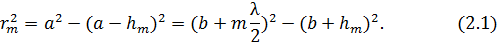
Раскроем скобки:
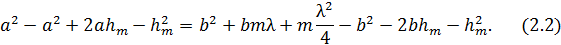
Приведем подобные члены в (2.2) и, учитывая, что квадрат длины волны – малая величина, которой можно пренебречь, найдем высоту сферического сегмента:
С учетом того что квадратом, высоты сферического сегмента ввиду его малой величины, тоже можно пренебречь, выражение для квадрата радиуса -й зоны (2.1) принимает вид
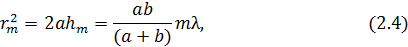
откуда радиус -й зоны Френеля
Вычислим площадь -й зоны Френеля, которая будет равна разности площадей сферических сегментов, выделяемых на волновом фронте внешними границами -й и 
-й зон Френеля. Площади сферических сегментов:
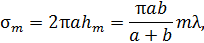
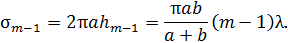
Тогда площадь -й зоны
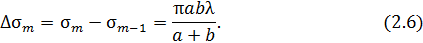
Как видим, значение площади зоны Френеля не зависит от ее порядкового номера, следовательно, площади всех зон одинаковы.
Поместим экран с круглым отверстием на пути распространения монохроматического света. Тогда число зон Френеля (для данной точки наблюдения), открываемых отверстием, можно определить, поделив площадь сферического сегмента, выделяемого отверстием, на площадь одной зоны. Если отверстие открывает четное число зон Френеля, то волны, идущие от двух соседних зон, при наложении погасят друг друга, и в рассматриваемой точке будет наблюдаться темное пятно, т. е. дифракционный минимум. Если же число зон нечетное, то в данной точке будет наблюдаться светлое пятно или дифракционный максимум.
Оценим, к примеру, число зон Френеля, умещающихся на полусфере радиусом = 10 см на расстоянии до экрана 
= 10 см для зеленого света длиной волны 500 нм. Площадь полусферы, равную 
, поделим на площадь одной зоны Френеля:
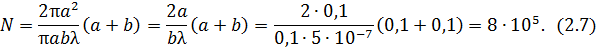
На полусфере умещается 800 000 зон Френеля! Радиус первой (центральной) зоны Френеля в рассмотренном примере будет приблизительно равен 0,16 мм. Поскольку освещенность в точке определяется действием половины центральной зоны Френеля, распространение света происходит внутри узкого канала радиусом, равным половине радиуса центральной зоны, т. е. прямолинейно.