Главная | Обратная связь

Дифракция Фраунгофера на круглом отверстии

Когда источник света и точка наблюдения бесконечно удалены от препятствия, вызвавшего дифракцию, наблюдается дифракция Фраунгофера. В этом случае волновой фронт будет представлять собой плоскость 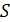, приведенную на рис. 2.6, где – точка наблюдения, – расстояние от плоскости 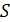до точки наблюдения .

Выделим на плоскости зоны Френеля, которые в данном случае будут представлять собой концентрические кольца (за исключением центральной зоны, которая является окружностью). Границей первой (центральной) зоны служат точки поверхности 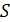, находящиеся на расстоянии

 

 

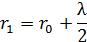
от точки . Точки и волнового фронта, находящиеся соответственно на расстояниях

 

 

 

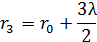
от точки , образуют границы второй, третьей и т. д. зон Френеля.

 

Рис. 2.6

При интерференции в точке лучи от двух соседних зон Френеля взаимно погасят друг друга, так как разность фаз этих волн будет равна .

Вычислим радиусы зон Френеля. Из выразим радиус первой зоны:

 

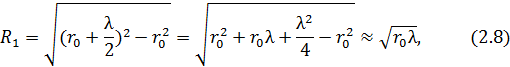
где - расстояние от точки до точки ; - длина волны света. (Слагаемым 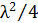пренебрегаем ввиду малой величины.)

Из аналогично выразим радиус второй зоны:

 

 

Из получим радиус третьей зоны

 

 

Следовательно, для любой -й зоны Френеля

 

 

где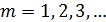

Радиусы зон Френеля, как следует из выражений (2.8)–(2.11) определяются значением длины волны и положением точки наблюдения. Так как первая зона Френеля – это круг радиусом , ее площадь

 

 

Все остальные зоны Френеля представляют собой концентрические кольца. Поэтому площадь второй зоны равна разности площадей кругов радиусами и , т. е.

 

 

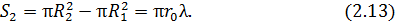
Площадь третьей зоны

 

 

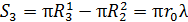
и т. д. Площадь -й зоны

 

 

Таким образом, площади всех зон Френеля одинаковы.

Волны, приходящие в точку от двух соседних зон, противоположны по фазе и при наложении гасят друг друга. Следовательно, амплитуду результирующей волны можно найти по формуле

 

 

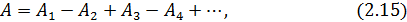
где , , , ... – амплитуды волн, приходящих в точку от первой, второй, третьей и т. д. зон Френеля. Чередование знаков «плюс» и «минус» вызвано тем, что волны от соседних зон Френеля приходят в противофазе.

Представим выражение (2.15) в следующем виде:

 

 

Можно считать амплитуды колебаний от соседних зон приблизительно равными, поэтому выражения, стоящие в скобках, равны нулю. Таким образом, амплитуда результирующей волны равна сумме (или разности) половин амплитуд волн от первой и последней зон Френеля. Знак «минус» соответствует четным , знак «плюс» – нечетным .

Если отверстие открывает четное число зон Френеля, амплитуда результирующей волны в точке будет равна нулю и в точке будет наблюдаться дифракционный минимум. Если отверстие открывает нечетноечисло зон Френеля, амплитуда результирующей волны будет равна сумме половин амплитуд волн от первой и последней зон и в точке М будет наблюдаться дифракционный максимум.

Амплитуда колебаний, приходящих в точку наблюдения от центральных и периферийных зон, убывает по мере удаления от центра волнового фронта (или по мере роста угла между направлением на точку наблюдения и нормалью к волновой поверхности). При достаточно большом количестве зон , и последним слагаемым в выражении (2.16) можно пренебречь. Таким образом, суммарная амплитуда от воздействия всего волнового фронта в точке наблюдения определяется действием только половины центральной зоны Френеля.