 |
|
Перестановки, инверсии, транспозиции.
Определение 1.Пусть  -
-  первых попарно различных натуральных чисел, т.е.
первых попарно различных натуральных чисел, т.е.  N,
N,  , если
, если  . Упорядоченный набор
. Упорядоченный набор  первых
первых  натуральных чисел будем называть перестановкой из
натуральных чисел будем называть перестановкой из  элементов.
элементов.
Перестановку  будем называть основной. Множество всех перестановок из
будем называть основной. Множество всех перестановок из  элементов будем обозначать так:
элементов будем обозначать так:  .
.
Пример 1.  - перестановка из четырёх элементов.
- перестановка из четырёх элементов.  - перестановка из семи элементов.
- перестановка из семи элементов.
Теорема 1. Число различных перестановок из  элементов равно
элементов равно  .
.
Доказательство проведём методом математической индукции по числу  .
.
База математической индукции.Пусть .Очевидно, существует единственная перестановка
.Очевидно, существует единственная перестановка  из одного элемента, т.е. для
из одного элемента, т.е. для  теорема верна.
теорема верна.
Индукционный переход. Докажем, что утверждение теоремы верно для перестановок из  - го элемента, если оно верно для перестановок из
- го элемента, если оно верно для перестановок из  элементов.
элементов.
Множество всех перестановок из  - го элемента разобьём на
- го элемента разобьём на  групп в зависимости от расположения в перестановке числа
групп в зависимости от расположения в перестановке числа  .
.
В 1 –ю группу включим все перестановки, в которых число  стоит на первом месте, т.е. перестановки вида
стоит на первом месте, т.е. перестановки вида  , в которых
, в которых  .
.
Во 2 –ю группу включим все перестановки, в которых число  стоит на втором месте, т.е. перестановки вида
стоит на втором месте, т.е. перестановки вида  , в которых
, в которых  и т.д.
и т.д.
В  –ю группу включим все перестановки, в которых число
–ю группу включим все перестановки, в которых число  стоит на последнем месте, т.е. перестановки вида
стоит на последнем месте, т.е. перестановки вида  , в которых
, в которых  .
.
Подсчитаем, сколько перестановок содержится в каждой такой группе. Если мы из каждой перестановки, входящей в  - ю группу, вычеркнем число
- ю группу, вычеркнем число  , то получившиеся перестановки будут образовывать всевозможные перестановки из
, то получившиеся перестановки будут образовывать всевозможные перестановки из  элементов, а их число по индукционному предположению равно
элементов, а их число по индукционному предположению равно 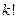 . Таким образом, получаем: число различных перестановок из
. Таким образом, получаем: число различных перестановок из  элементов равно
элементов равно  .
.
Определение 2. Операцию, при которой меняются местами два элемента перестановки (не обязательно соседние), будем называть транспозицией.
Пример 2.Например: .В этой перестановке совершили одну транспозицию: поменяли местами 1 и 2.
.В этой перестановке совершили одну транспозицию: поменяли местами 1 и 2.
Определение 3. Если в перестановке  пара чисел
пара чисел  и
и  расположены так, что большее предшествует меньшему (т.е.
расположены так, что большее предшествует меньшему (т.е.  ), то говорят, что пара чисел
), то говорят, что пара чисел  ,
,  в этой перестановке образует инверсию(беспорядок.)
в этой перестановке образует инверсию(беспорядок.)
Пример 3.Например, в перестановке  числа 2 и 1образуют инверсию, т.к.
числа 2 и 1образуют инверсию, т.к.  и 2 предшествует 1. В этой перестановке числа 4 и 1такжеобразуют инверсию.
и 2 предшествует 1. В этой перестановке числа 4 и 1такжеобразуют инверсию.
Определение 4. Число пар, образующих инверсию в данной перестановке, называется числом инверсий данной перестановки и обозначается так:  .
.
Определение 5. Перестановка называется чётной, если число инверсий этой перестановки чётное. Перестановка называется нечётной, если число инверсий этой перестановки нечётное.
Чтобы подсчитать число инверсных пар перестановки, подсчитаем сначала число пар, образующих инверсию, в состав которых входит 1.
Очевидно, таких пар столько, сколько чисел стоит перед единицей. Теперь подсчитаем число пар, образующих инверсию, в состав которых входит 2 (и не входит 1). Очевидно, таких пар столько, сколько не вычеркнутых чисел стоит перед двойкой, и т.д.
Пример 4.Подсчитаем количество инверсий в перестановке  . Единица первая, следовательно, ни с одним из чисел инверсий не образует, и единицу вычёркиваем. Перед двойкой теперь стоят два не вычеркнутые числа. Следовательно, число 2 образует инверсию и с 3, и с 4, и двойку вычёркиваем. Перед тройкой не вычеркнутых чисел нет. Таким образом,
. Единица первая, следовательно, ни с одним из чисел инверсий не образует, и единицу вычёркиваем. Перед двойкой теперь стоят два не вычеркнутые числа. Следовательно, число 2 образует инверсию и с 3, и с 4, и двойку вычёркиваем. Перед тройкой не вычеркнутых чисел нет. Таким образом, 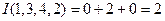 . Следовательно, перестановка
. Следовательно, перестановка  чётная.
чётная.
Без доказательства приведём следующую теорему.
Теорема 2.Транспозиция любых двух элементов перестановки меняет чётность перестановки на противоположную.
Следствие. Чётное число транспозиций не меняет чётность перестановки. Нечётное число транспозиций меняет чётность перестановки на противоположную.
Теорема 3. Число различных чётных перестановок из  элементов равно числу различных нечётных перестановок из
элементов равно числу различных нечётных перестановок из  элементов и равно
элементов и равно  .
.
Доказательство. Обозначим через 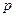 и
и  соответственно число различных чётных и нечётных перестановок из
соответственно число различных чётных и нечётных перестановок из  элементов. В каждой из
элементов. В каждой из
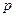 чётных перестановок поменяем местами первые два элемента. По теореме 2 все полученные таким образом перестановки являются нечётными, причём различными. Следовательно,
чётных перестановок поменяем местами первые два элемента. По теореме 2 все полученные таким образом перестановки являются нечётными, причём различными. Следовательно,  . Аналогично доказываем, что
. Аналогично доказываем, что  , откуда и получаем:
, откуда и получаем:  .
.
Тогда  .
.
§7. Определение определителя  - го порядка.
- го порядка.
Определение 1. Определителемквадратной матрицы 
 K
K 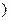 порядка
порядка  называется число, равное алгебраической сумме всевозможных произведений элементов матрицы, взятых по одному из каждой строки и по одному из каждого столбца. Слагаемое берётся со знаком плюс, если перестановка вторых индексов чётная, при условии, что первые индексы стоят в порядке возрастания. Слагаемое берётся со знаком минус, если перестановка вторых индексов нечётная, при условии, что первые индексы стоят в порядке возрастания.
называется число, равное алгебраической сумме всевозможных произведений элементов матрицы, взятых по одному из каждой строки и по одному из каждого столбца. Слагаемое берётся со знаком плюс, если перестановка вторых индексов чётная, при условии, что первые индексы стоят в порядке возрастания. Слагаемое берётся со знаком минус, если перестановка вторых индексов нечётная, при условии, что первые индексы стоят в порядке возрастания.
Определитель квадратной матрицы  -го порядка называют определителем
-го порядка называют определителем  -го порядка.
-го порядка.
Замечание 1. Определитель имеет смысл только для квадратной матрицы. Если
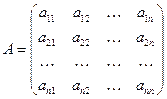 , то определитель матрицы
, то определитель матрицы 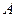 обозначают так:
обозначают так:  или так:
или так:
 . Очевидно,
. Очевидно,  K.
K.
Запишем словесное определение с помощью формулы. В каждое слагаемое определителя входит сомножителем один элемент из каждой строки матрицы. Следовательно, каждое слагаемое можно записать так: 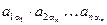 . Вторые индексы сомножителей в этом произведении образуют перестановку, т.к. в это произведение входит сомножителем один элемент из каждого столбца. Поскольку определитель равен сумме всевозможных таких слагаемых, то таких слагаемых столько, сколько различных перестановок из
. Вторые индексы сомножителей в этом произведении образуют перестановку, т.к. в это произведение входит сомножителем один элемент из каждого столбца. Поскольку определитель равен сумме всевозможных таких слагаемых, то таких слагаемых столько, сколько различных перестановок из  элементов, т.е.
элементов, т.е.
 .
.
По определению определителя слагаемое  берётся со знаком плюс, если перестановка
берётся со знаком плюс, если перестановка  чётная, и со знаком минус в противном случае. Таким образом, слагаемое
чётная, и со знаком минус в противном случае. Таким образом, слагаемое 
берётся со знаком  , где
, где  Z.
Z.
Таким образом, определение определителя квадратной матрицы  порядка
порядка  может быть записано так:
может быть записано так:
 .
.
В этой формуле суммирование ведётся по всевозможным перестановкам  из
из  элементов.
элементов.
Покажем теперь, что данные выше определения определителей 2-го и 3-го порядков являются частными случаями определения определителя  -го порядка.
-го порядка.
Пример 1. Рассмотрим определитель 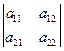 . Выберем элементы из первой строки матрицы этого определителя. Это могут быть
. Выберем элементы из первой строки матрицы этого определителя. Это могут быть  или
или  . Если из первой строки выбрали
. Если из первой строки выбрали  , то из второй строки можно выбрать только
, то из второй строки можно выбрать только  , т.к. первый столбец уже «занят» (
, т.к. первый столбец уже «занят» (  стоит в первом столбце).
стоит в первом столбце).
Если из первой строки выбрали  , то из второй строки можно выбрать только
, то из второй строки можно выбрать только  , т.к. второй столбец уже «занят» (
, т.к. второй столбец уже «занят» (  стоит во втором столбце).
стоит во втором столбце).
Теперь выясним, с каким знаком входит каждое из этих произведений в определитель. В обоих произведениях 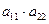 и
и  сомножители стоят в порядке возрастания номеров строк. Поэтому нужно найти число инверсий в перестановках
сомножители стоят в порядке возрастания номеров строк. Поэтому нужно найти число инверсий в перестановках  и
и 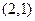 . Очевидно,
. Очевидно,  . Следовательно,
. Следовательно, 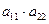 берем со знаком плюс, а
берем со знаком плюс, а  - со знаком минус. Таким образом,
- со знаком минус. Таким образом,  , что совпадает с определением определителя 2-го порядка, данным ранее.
, что совпадает с определением определителя 2-го порядка, данным ранее.
Пример 2. Рассмотрим определитель  . Выберем элементы из первой строки матрицы этого определителя. Это могут быть
. Выберем элементы из первой строки матрицы этого определителя. Это могут быть  ,
,  или
или  . Если из первой строки выбрали
. Если из первой строки выбрали  , то из второй строки можно выбрать
, то из второй строки можно выбрать  или
или  , т.к. первый столбец уже «занят» (
, т.к. первый столбец уже «занят» (  стоит в первом столбце).
стоит в первом столбце).
Если из первой строки выбрали  , то из второй строки можно выбрать
, то из второй строки можно выбрать  или
или  , т.к. второй столбец уже «занят» (
, т.к. второй столбец уже «занят» (  стоит во втором столбце).
стоит во втором столбце).
Если из первой строки выбрали  , то из второй строки можно выбрать
, то из второй строки можно выбрать  или
или  , т.к. третий столбец уже «занят» (
, т.к. третий столбец уже «занят» (  стоит в третьем столбце).
стоит в третьем столбце).
Если после выбора элементов в двух первых строках получили произведение 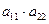 , то в третьей строке можно выбрать только
, то в третьей строке можно выбрать только  , т.к. первый и второй столбцы уже «заняты» (
, т.к. первый и второй столбцы уже «заняты» (  стоит в первом столбце , а
стоит в первом столбце , а  - во втором столбце). Таким образом, получим произведение
- во втором столбце). Таким образом, получим произведение  .
.
Рассуждая аналогичным образом получим ещё пять слагаемых:  .
.
Теперь выясним, с каким знаком входит каждое из этих произведений в определитель. Во всех произведениях сомножители стоят в порядке возрастания номеров строк. Поэтому нужно найти число инверсий в перестановках вторых индексов. Очевидно,  .
.
Следовательно, со знаком плюс берем произведения  ,
,  ,
,  .
.
Остальные произведения, т.е.  берём со знаком минус.
берём со знаком минус.
Таким образом,  , что совпадает с определением определителя 3-го порядка, данным ранее.
, что совпадает с определением определителя 3-го порядка, данным ранее.
Определение 2. Квадратную матрицу  порядка
порядка  будем называть верхней треугольной, если все
будем называть верхней треугольной, если все
её элементы, стоящие «под главной диагональю», равны нулю. Другими словами, если  при условии, что
при условии, что  .
.
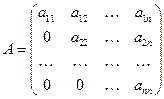 - верхняя треугольная матрица.
- верхняя треугольная матрица.
Определение 3. Квадратную матрицу  порядка
порядка  будем называть нижней треугольной, если все
будем называть нижней треугольной, если все
её элементы, стоящие «над главной диагональю», равны нулю. Другими словами, если  при условии, что
при условии, что  .
.
 - нижняя треугольная матрица.
- нижняя треугольная матрица.
Общее название верхних треугольных и нижних треугольных матриц – треугольные матрицы.
Теорема. Определитель треугольной матрицы равен произведению её диагональных элементов, т.е.
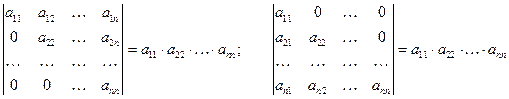 .
.
Доказательство проведём для верхних треугольных матриц. Для нижних треугольных матриц доказательство проводится аналогично.
Если какой-то элемент матрицы равен нулю, то слагаемое, в котором этот элемент является сомножителем, равно нулю и потому его можно не учитывать. Выберем в первом столбце  , т.к. в этом столбце только
, т.к. в этом столбце только  не равен нулю. Во втором столбце выберем
не равен нулю. Во втором столбце выберем  , т.к. первая строка уже «занята», а элементы всех остальных строк во втором столбце равны нулю. Рассуждая таким образом, выберем элементы в первых
, т.к. первая строка уже «занята», а элементы всех остальных строк во втором столбце равны нулю. Рассуждая таким образом, выберем элементы в первых  столбцах и получим произведение
столбцах и получим произведение 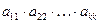 . В
. В  - м столбце выберем
- м столбце выберем  , т.к. первые
, т.к. первые  строк уже «заняты», а элементы всех остальных строк в
строк уже «заняты», а элементы всех остальных строк в  - м столбце равны нулю, и т.д. В результате получим произведение диагональных элементов
- м столбце равны нулю, и т.д. В результате получим произведение диагональных элементов  . Эти элементы расположены в порядке возрастания номеров строк. Поэтому остаётся найти число инверсий в перестановке
. Эти элементы расположены в порядке возрастания номеров строк. Поэтому остаётся найти число инверсий в перестановке  , которое, очевидно, равно нулю. Следовательно, это произведение берём со знаком плюс, и теорема доказана.
, которое, очевидно, равно нулю. Следовательно, это произведение берём со знаком плюс, и теорема доказана.