Главная | Обратная связь

ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ.

 

Рассмотрим нормальную систему обыкновенных дифференциальных уравнений, описывающих динамику некоторого объекта

, (2)

где - фазовые переменные - переменные, определяющие состояние объекта (для механических систем фазовые переменные - это чаще всего координаты и скорости), - функции, определенные в открытой области действительного или комплексного пространства для всех моментов времени из .

Эту систему можно записать в виде векторного уравнения

(3)

Где .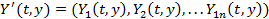

Будем предполагать, что вектор-функция в области непрерывна по и имеет непрерывные частные производные первого порядка по . Когда y может принимать комплексные значения, функцию будем предполагать аналитической относительно

При этих условиях справедлива теорема Коши о существовании в области Z единственной интегральной кривой системы для каждой точки . Задавая начальное условие

, (4)

получаем единственное частное решение (невозмущенное движение)

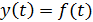. (5)

 

На практике обеспечить выполнение начальных условий идеально точно никогда не удается, вследствие чего движение объекта начинается не из точки (4), а из некоторой более или менее малой ее окрестности. Таким образом, в действительности, согласно теореме о существовании и единственности решения уравнения (3) имеем не решение (5), а некоторое другое решение , начальное значение которого является некоторой точкой этой окрестности. 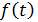Возникает вопрос – будут ли близки и на больших промежутках времени, если были близки их начальные значения?

В соответствии с теоремой о непрерывной зависимости решения дифференциальных уравнений от начальных условий такая близость будет иметь место для конечных промежутков времени. Однако, если устремить время к бесконечности, эта теорема не может дать ответ на поставленный вопрос. Тогда задача превращается в задачу теории устойчивости – можно ли, задавшись некоторым, в том числе сколь угодно малым числом ε>0 найти такое число δ(ε)>0, что все решения системы (3), начинающиеся из δ-окрестности точки , при любом не выйдут из ε-окрестности решения (5)?

Определение 1. Решение (невозмущенное движение) системы (3) назовем устойчивым (в смысле Ляпунова) по переменным 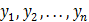, если для любых ε>0 и ) можно указать такое, что все решения (возмущенные движения ), удовлетворяющие условию определены в промежутке (т.е. при 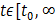) и для всех t из этого промежутка будут удовлетворять неравенству (здесь означает норму – в простейшем случае длину соответствующего вектора; например, евклидова норма вектора ).

С использованием кванторов 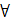- « для всех» и 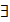- «существует» определение 1 можно переписать в следующем виде:

 

Определение 2. Решение (невозмущенное движение) называется устойчивым равномерно по времени в области Т, если для любого числа ε>0 можно выбрать зависящее только от ε число δ>0 (независящее от начального момента 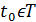) такое, что при любых начальных возмущениях, удовлетворяющих неравенству .

Очевидно, что для автономных систем (2), правые части которых не зависят явно от времени, и для систем с периодическими коэффициентами устойчивость всегда будет равномерной по .

 

Определение 3. Если для некоторых ε>0 и и любых δ>0 существуют решение (хотя бы одно) и момент такие, что при выполняется 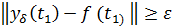, то движение неустойчиво по .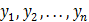

 

Определение 4. Решение называется асимптотически устойчивым по переменным (в смысле Ляпунова) при , если:

· это решение устойчиво по Ляпунову;

· для любого существует такое, что все решения , удовлетворяющие условию

, (6)

обладают свойством

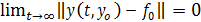. (7)

Неравенство (6) при фиксированном определяет область притяжения решения .

 

Определение 5. Если решение устойчиво по Ляпунову и соотношение (7) справедливо при любых , определяемых любыми начальными условиями (или 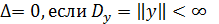) во всем фазовом пространстве переменных системы (3), то решение асимптотически устойчиво в целом по переменным

 

Упражнения:

 

1. Переформулировать все определения для устойчивости тривиального решения

2. Доказать следующие теоремы об устойчивости линейных систем:

Теорема 1. Любое решение однородной системы линейных дифференциальных уравнений

(8)

устойчиво тогда и только тогда, когда устойчиво ее тривиальное решение.

Теорема 2. Линейная неоднородная система уравнений

устойчива тогда и только тогда, когда устойчива соответствующая ей однородная система уравнений. Здесь 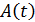- матрица.

Указания: 1. Использовать определения устойчивости тривиального решения однородной системы и произвольного решения однородной и неоднородной систем.

2. Применить следующее свойство решений линейных систем: сумма (разность) двух решений однородной линейной системы есть решение этой системы; разность двух решений неоднородной системы есть решение однородной системы.

Замечание: Из теорем 1 и 2 следует, что у линейных систем дифференциальных уравнений либо все решения одновременно устойчивы, либо все решения неустойчивы. Поэтому для таких уравнений можно говорить об устойчивой или неустойчивой системе. Для нелинейных же дифференциальных уравнений не имеет смысла говорить об устойчивости системы, так как некоторые решения могут быть устойчивыми, а другие решения той же системы уравнений – неустойчивыми.

Определение 6. Решение (невозмущенное движение) называется устойчивым асимптотически равномерно по времени и начальным возмущениям из области притяжения , если оно асимптотически устойчиво и для любого можно найти Т(η) такое, что при всех , каковы бы ни были и из области притяжения.

Для автономных систем устойчивость всегда равномерна относительно начальных данных.

Определение 7. Устойчивость по части переменных.

Допустим, что уравнения движения системы приведены к нормальному виду

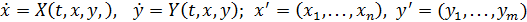(9)

 

Обозначим 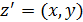. Пусть функции определены в области

 

(10)

Причем и 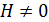суть постоянные, , а в области (10) разлагаются в сходящиеся степенные ряды по целым степеням переменных с вещественными ограниченными коэффициентами, непрерывными по отношению к .

Решение z=0 системы (9) устойчиво по отношению к переменным x, если при всяком произвольно задаваемом числе , как бы мало оно ни было, может быть выбрано положительное число 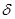, так, чтобы при всяких возмущениях , удовлетворяющих условию , и при всяком , было выполнено , т.е. для заданных найдется такое , что для всех 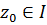и всех .

Определение 8. Устойчивость при постоянно действующих возмущениях.

В практических задачах уравнения (3) являются математической моделью некоторого объекта, которая не может быть построена идеально точно. Всегда остаются неучтенные в уравнениях (3) члены , о которых известно только то, что они не нарушают условий теорем существования и единственности решений дифференциальных уравнений и малы по сравнению с явно фигурирующими в уравнениях (3) членами. Поэтому движение объекта происходит на самом деле при постоянно действующих возмущениях . Можно ввести следующее определение: невозмущенное движение устойчиво при постоянно действующих возмущениях , если для всякого числа 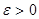, как бы мало оно ни было, существуют два других числа 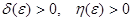таких, что всякое решение уравнений

,

удовлетворяющее при неравенству , при удовлетворяет неравенствам 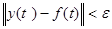, каковы бы ни были функции , удовлетворяющие в области неравенству .

Определенная таким образом устойчивость при постоянно действующих возмущениях является непосредственным обобщением устойчивости по отношению к возмущениям начальных условий, т.е. к возмущениям, которые действовали только в начале движения. Реальная система обычно находится под постоянным действием небольших (и в силу этого не учтенных в модели) сил. Поэтому введенное выше определение (впервые такую устойчивость рассмотрел Н.Г. Четаев) имеет наибольшее практическое значение. Но теория устойчивости по Ляпунову при этом совершенно не обесценивается, так как методы Ляпунова пригодны также для исследования устойчивости при постоянно действующих возмущениях, а в практически наиболее важных случаях эта задача непосредственно приводится к задаче об устойчивости по Ляпунову. Для установившихся и периодических движений достаточным условием устойчивости при постоянно действующих возмущениях является асимптотическая устойчивость по Ляпунову [5].

 

3.МЕТОДЫ РЕШЕНИЯ ЗАДАЧ УСТОЙЧИВОСТИ

1. В случаях, когда можно получить общее решение системы (3), устойчивость решения можно установить исходя из определения. При построении фазового портрета системы наглядно видны устойчивые и неустойчивые равновесия и траектории.

Пример. Определить, будет ли устойчивым неограниченное решение скалярного уравнения

.

Чаще всего мы не можем получить общее решение или построить фазовый портрет системы. В таких случаях для решения вопроса об устойчивости можно воспользоваться разработанным А.М. Ляпуновым так называемым первым методом – методом построения решений в виде особых бесконечных рядов. Но этот метод, полностью решающий вопрос об устойчивости во многих классических задачах, очень сложен в теоретическом отношении, и для практических целей, как отмечал и сам Ляпунов, гораздо удобнее пользоваться другими методами.

2. Устойчивость линейных систем с постоянными коэффициентами всегда можно установить по корням характеристического уравнения, так как общее решение таких систем определяется корнями этого уравнения.

 

Справедливы теоремы [3, 5, 6]:

Теорема 1. Линейная однородная система (8) с постоянной матрицей А устойчива тогда и только тогда, когда все корни характеристического уравнения матрицы А, т.е. корни уравнения обладают неположительными вещественными частями, причем корни, имеющие нулевые вещественные части, допускают лишь простые элементарные делители.

Теорема 2. Линейная однородная дифференциальная система с постоянной матрицей А асимптотически устойчива тогда и только тогда, когда все корни характеристического уравнения матрицы А имеют отрицательные вещественные части.

Необходимые и достаточные условия, при которых алгебраическое уравнение с действительными коэффициентами

(11)

имеет корни только с отрицательными вещественными частями, т.е. , дает следующий

Критерий Гурвица [3, 5, 6]:

Для того чтобы для всех корней уравнения (11) выполнялось условие 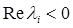, необходимо и достаточно, чтобы были положительны все главные диагональные миноры матрицы Гурвица

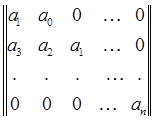
Укажем также следующее простое необходимое условие : если и если для всех корней уравнения (11) , то все коэффициенты уравнения (11) положительны.

Для линейных систем при определенном расположении корней характеристического уравнения все решения устойчивы (асимптотически устойчивы) или все решения неустойчивы.

Для нелинейных систем все обстоит гораздо сложнее. Некоторые решения таких систем могут быть устойчивыми, а другие – неустойчивыми. Так как чаще всего нам не удается получить всю совокупность решений нелинейных систем, то при исследовании устойчивости отдельного решения (невозмущенного движения) для исследования поведения возмущенных решений удобно составлять уравнения возмущенного движения (по терминологии А.М.Ляпунова).

 

4. УРАВНЕНИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ [3, 5, 6]

 

Проведем в системе (3) замену переменных 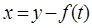. В новых переменных будем иметь

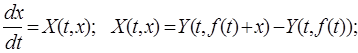(12)

причем .

Система (12) определяет дифференциальные уравнения возмущенного движения. Движение 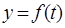при такой замене переходит в положение равновесия системы (12).

 

Исследование устойчивости по первому приближению.

Для исследования устойчивости отдельного решения нелинейной системы можно составить уравнения возмущенного движения, выделить в них первое приближение. Если рассматриваются автономные системы (время явно не входит в правые части), то затем можно воспользоваться следующими теоремами А.М.Ляпунова об асимптотической устойчивости и неустойчивости по первому приближению:

Теорема 1. Если все корни характеристического уравнения системы первого приближения уравнений возмущенного движения имеют отрицательные вещественные части, то невозмущенное движение устойчиво асимптотически при любых нелинейных членах полных уравнений возмущенного движения.

Теорема 2. Если хотя бы один корень характеристического уравнения системы первого приближения уравнений возмущенного движения имеет положительную вещественную часть, то невозмущенное движение неустойчиво при любых нелинейных членах полных уравнений возмущенного движения.

При исследовании устойчивости по первому приближению неасимптотическая устойчивость для нелинейных систем может иметь место только в критических по Ляпунову случаях, когда вещественные части некоторых корней характеристического уравнения обращаются в нуль, а остальные его корни имеют отрицательные вещественные части.

В таких случаях нельзя получить достаточные условия устойчивости по первому приближению, рассмотрение первого приближения недостаточно для полного решения вопроса об устойчивости. Но в этих случаях можно получить необходимые условия устойчивости – условия, при нарушении которых движение становится неустойчивым. Это условия, при которых отсутствуют корни характеристического уравнения системы первого приближения с положительными вещественными частями.

В критических случаях достаточные условия устойчивости можно получить с помощью метода функций Ляпунова, а также с помощью специальной теории критических случаев[1, 5].

 

5. МЕТОД ФУНКЦИЙ ЛЯПУНОВА [5, 6]

 

Как отмечает А.М.Ляпунов «…Все наиболее интересные и важные вопросы механики (как, например, те, которые приводят к каноническим уравнениям) таковы, что в особенных случаях, когда первое приближение недостаточно, задача делается для них в высшей степени трудною. И пока невозможно указать каких-либо приемов для ее решения. Случаи этого рода весьма разнообразны, и в каждом из них задача получает свой особый характер, так что не может быть и речи о каких-либо общих методах ее решения, которые относились бы ко всем таким случаям. Известно, что существуют случаи, когда рассматриваемая задача допускает приведение к некоторой задаче о максимумах . . . Всем известна теорема Лагранжа об устойчивости равновесия . . . и изящное доказательство, предложенное для нее Лежен Дирихле. Последнее основывается на соображениях, которые могут послужить для доказательства многих подобных теорем » [1].

Руководствуясь такими соображениями, А.М. Ляпунов разработал так называемый второй метод исследования устойчивости - метод функций Ляпунова. Метод функций Ляпунова, еще называемый прямым методом – один из наиболее эффективных методов решения задач устойчивости. А.М.Ляпунов предложил, не отыскивая решений уравнений возмущенного движения, строить некоторые функции, по изменению которых вдоль траекторий уравнений возмущенного движения можно делать вывод об устойчивости невозмущенного движения.

Если заключение об асимптотической устойчивости делать по первому приближению, то в силу доказательства теоремы Ляпунова об устойчивости по первому приближению мы можем утверждать, что невозмущенное движение будет асимптотически устойчиво только при малых начальных отклонениях (так называемая «устойчивость в малом»). Множество точек, притягиваемых при к невозмущенному движению, т.е. область притяжения, может оказаться весьма ограниченной. Но область притяжения в действительности может быть и большой, только оценки, получаемые при исследовании по первому приближению, дают почти непригодные с точки зрения практики результаты.

Поэтому даже в тех случаях, когда устойчивость можно установить по первому приближению, построение функции Ляпунова поможет дать хорошую оценку области притяжения, оценку решения, т.е. переходного процесса, и оценку времени переходного процесса.

«Заметим, что для всякой системы дифференциальных уравнений любая определенно-положительная функция может служить функцией Ляпунова . . . Требуя, чтобы в силу данной системы производная по времени от этой функции была знакоотрицательной, можно выписать какие-то условия устойчивости нулевого решения системы. При неосторожном выборе функции Ляпунова эти условия могут оказаться противоречивыми. Кроме того, если встать на такой путь рассуждений, мы неизбежно утонем в океане малоценных достаточных условий устойчивости, весьма далеких от того, чтобы быть необходимыми. Хорошо проверенным критерием оценки полученной функции Ляпунова является следующее требование: достаточные условия, полученные с помощью этой функции в нелинейном случае (для полной системы), должны быть необходимыми в линейном случае» [7] (полученными по первому приближению).

 

6. МЕТОД ФУНКЦИЙ ЛЯПУНОВА ДЛЯ АВТОНОМНЫХ СИСТЕМ

 

Рассмотрим некоторые вещественные однозначные, непрерывные вместе с производными в области

(13)

функции , причем .

Определение 9. Функция 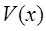называется знакопостоянной (положительной или отрицательной) в области (13), если во всех точках области она принимает значения только одного знака (нулевое значение она может принимать не только в начале координат).

Определение 10. Функция 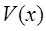называется знакоопределенной (определенно-положительной) в области (13) , если во всех точках области, кроме начала координат, она принимает значения строго только одного знака (больше нуля).

Примеры: 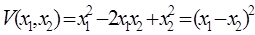функция знакопостоянная положительная, так как она обращается в нуль не только в начале координат, но и на прямой .

Функция в пространстве трех переменных является знакоположительной: она равна нулю не только в начале координат, но и на прямой . В пространстве же двух переменных эта функция является определенно-положительной.