 |
|
Теоремы о неустойчивости движения
Во всех теоремах об устойчивости в первую очередь требовалась знакоопределенность функции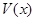 
(чтобы обеспечить замкнутость поверхностей уровня этой функции), а уже после этого накладывались условия на знак ее производной. В теоремах же о неустойчивости в первую очередь рассматривается знакоопределенность (знакопостоянство) производной функции Ляпунова в силу уравнений возмущенного движения, чтобы обеспечивать необходимый для доказательства неустойчивости уход изображающей точки из окрестности начала координат за счет неограниченного роста функции 
.
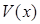В первой теореме о неустойчивости – теореме Ляпунова, - требуется знакоопределенность производной, а затем это условие ослабляется – сначала до знакопостоянства (теорема Красовского о неустойчивости). Далее условие на соотношение знаков самой функции и ее производной в силу уравнений возмущенного движения накладывается только в определенной части фазового пространства (теорема Четаева о неустойчивости). Все это становится понятным, если получить определение неустойчивости как отрицание определения устойчивости, записанного с помощью кванторов. Для этого, как известно, в ранее приведенном определении устойчивости следует поменять местами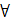 
- « для всех» и 
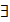- «существует», а знак неравенства в заключении определения поменять на противоположный. В результате получим:
Таким образом, для доказательства неустойчивости достаточно обнаружить единственную траекторию с начальным условием из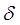 
- окрестности, уходящую в момент 
из 
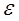-окрестности начала координат.
Первая теорема Ляпунова о неустойчивости: если для уравнений возмущенного движения возможно найти функцию 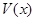такую,что ее полная производная по времени (14) есть функция знакоопределенная, а сама функция 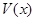не будет знакопостоянной знака, противоположного с 
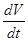, то невозмущенное движение неустойчиво.
Теорема Красовского о неустойчивости: если для дифференциальных уравнений возмущенного движения можно найти такую функцию, что ее производная в силу этих уравнений (14) знакоположительна, причем многообразие точек, для которых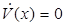 
не содержит целых траекторий системы, кроме начала координат, при 
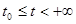, и если в любой сколь угодно малой окрестности начала координат существуют точки, для которых 
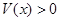, то невозмущенное движение неустойчиво.
Теорема Четаева о неустойчивости: Если дифференциальные уравнения возмущенного движения позволяют найти функцию 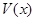, для которой в сколь угодно малой окрестности нуля существует область 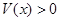, ограниченная поверхностью 
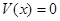, проходящей через начало координат, и если производная (14) положительна во всех точках области 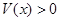, то невозмущенное движение неустойчиво.
Замечание о знакоопреденности функций.
Определение 11. Функция 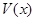называется однородной формой степени m , если 
при произвольном 
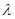. Очевидно, знакоопределенность форм может иметь место только при четном m ( так как только тогда знак 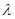не влияет на знак 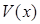). При этом минимальной степенью является m=2 . Понятно также, что в разложении любой функции в окрестности начала координат можно выделить формы первого порядка 
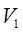, второго порядка 
и т. д.
При малых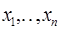 
знак функции 
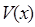определяется членами низшего порядка в ее разложении, т.е. формой низшего порядка. Поэтому разложение знакоопределенной функции может начинаться только с форм четного порядка. К сожалению, критерий знакоопределенности таких форм известен только для квадратичных форм – это хорошо известный критерий Сильвестра – матрица коэффициентов квадратичной формы должна быть знакоопределенной.
Критерий Сильвестра: для того, чтобы квадратичная форма была определенно-положительной, необходимо и достаточно, чтобы все главные диагональные миноры матрицы ее коэффициентов были положительны.
Метод Четаева построения функций Ляпунова в виде связки интегралов. Общих методов построения функций, удовлетворяющих условиям теорем прямого метода Ляпунова нет. Приведем один из наиболее сильных методов построения таких функций.
Пусть уравнения возмущенного движения допускают первый интеграл
. (15)
Если разность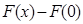 
является определенно-положительной функцией переменных 
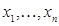, то в качестве функции Ляпунова можно взять 
= 
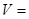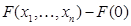. Производная этой функции по времени в силу уравнений возмущенного движения равна нулю согласно определению интеграла и, следовательно, такая функция удовлетворяет всем условиям теоремы Ляпунова об устойчивости движения.
В некоторых случаях уравнения возмущенного движения допускают несколько первых интегралов:
, . . . , 
,
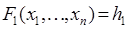где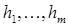 
- постоянные интегрирования. Пусть ни один из них не является знакоопределенной функцией. Для таких систем Н.Г. Четаев предложил строить функцию Ляпунова с помощью связки интегралов
,
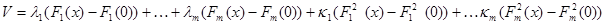где 
- неопределенные постоянные, выбором которых нужно распорядиться так, чтобы полученная функция была знакоопределенной. Если это удастся сделать, то, согласно теореме Ляпунова будем иметь устойчивость невозмущенного движения, поскольку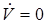 
.
При построении связки интегралов один из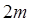 
коэффициентов 
можно выбрать произвольно, например, положив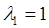 
. Часто функцию 
можно выбрать в виде линейной связки интегралов, положив все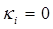 
, подбирая остальные коэффициенты так, чтобы линейные члены в разложении полученной функции в ряд в окрестности начала координат обращались в нуль.
Во многих механических задачах интегралы уравнений движения можно построить при помощи общих теорем механики, не составляя самих уравнений. Понятно, что этот прием позволяет значительно упростить решение задачи об устойчивости.