Главная | Обратная связь

ЗАКОНИ РОЗПОДІЛУ ЇХ ІМОВІРНОСТЕЙ

ТЕМА 1. ВИПАДКОВІ ВЕЛИЧИНИ

 

Величина називається випадковою, якщо вона в результаті події приймає значення наперед невідоме. Випадкові величини бувають дискретні та неперервні.

Дискретною випадковою величиною (ДВВ) називається така випадкова величина, можливі значення якої утворюють рахункову множину скінчену або нескінчену. Можливі значення ДВВ є окремо ізольовані числа, які ця величина приймає з певними ймовірностями. Іншими словами, можливі значення ДВВ можна пронумерувати. Число можливих значень ДВВ може бути скінченим або нескінченим.

Неперервною випадковою величиною (НВВ) називається така випадкова величина, можливі значення якої належать деякому інтервалу скінченому чи нескінченому.

Для опису випадкової величини необхідно навести не лише множину можливих її значень, а й указати, з якими ймовірностями ця величина набуває того чи іншого можливого значення.

З цією метою вводять поняття закону розподілу ймовірностей.

Співвідношення, що встановлює зв’язок між можливими значеннями випадкової величини та відповідними ймовірностями, називають законом розподілу випадкової величини.

Закон розподілу дискретної випадкової величини Х можна задати в аналітичній, табличній формі або графічно.

У разі табличної форми запису закону розподілу подається послідовність можливих значень випадкової величини Х, які розміщені у порядку зростання, та відповідних ймовірностей. Табличну форму запису закону розподілу називають рядом розподілу:

 

				…
				…

 

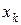
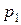
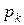
Оскільки випадкові події і є між собою несумісними і утворюють повну групу 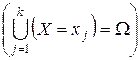, то ряд розподілу має наступну властивість:

. (1)

Рівність (1) називають умовою нормування для дискретної випадкової величини Х.

Закон розподілу ймовірностей можна унаочнити графічно. Для цього візьмемо систему координат 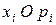, відкладемо на осі абсцис можливі значення випадкової величини , а на осі ординат – ймовірності цих можливих значень, потім точки з координатами 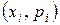послідовно сполучимо відрізками прямої. Утворену при цьому фігуру, називають імовірнісним многокутником або многокутником розподілу.

Приклад 1. ­Закон розподілу дискретної випадкової величини Х задано у табличній формі:

	-2,5		3,5		6,5
	0,1	0,2	0,1	0,3	0,2	0,1

Побудувати многокутник розподілу.

Розв’язання: Многокутник розподілу зображено на рисунку 1

 

 

 

Рисунок 1

Сума ординат імовірнісного многокутника завжди дорівнює одиниці. ­

Закон розподілу ймовірностей можна подати в формі, яка придатна і для дискретних і для неперервних випадкових величин, а саме як функцію розподілу випадкової величини . Її називають ще інтегральною функцією розподілу.

Функцією розподілу ймовірностей називається така функція , яка для кожного аргументу х визначає ймовірність того, що випадкова величина Х менше цього аргументу х:

. (2)

Властивості функції розподілу випливають із її означення.

1. . (3)

2. є не спадаючою функцією: якщо , тоді .

3. Імовірність того, що випадкова величина Х набуде можливого значення 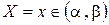, дорівнює приросту інтегральної функції на цьому проміжку:

. (4)

4. Якщо випадкова величина Х є неперервною, то ймовірність того, що вона набуде конкретного можливого значення, завжди дорівнює нулю:

.

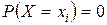І справді, поклавши в (4) , , дістанемо

.

Коли 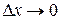, маємо

.

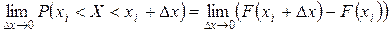Оскільки при 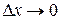, то

,

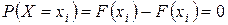що і потрібно було довести.

Отже для НВВ Х справджуються такі рівності:

.

5. Якщо , виконуються два подані далі співвідношення:

1) . (5) Оскільки подія полягає в тому, що випадкова величина Х набуває числового значення, яке міститься ліворуч від . А така подія є неможливою.

2) . (6)

Подія полягає в тому, що випадкова величина Х набуває числового значення, яке міститься ліворуч від . Ця подія є вірогідною, оскільки будь-яке число .

6. Функція розподілу неперервна зліва:

, .

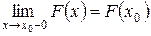7. Якщо можливі значення випадкової величини Х належать обмеженому проміжку , то

для

для

Ця властивість є наслідком властивості 5.

Приклад 2. Закон розподілу дискретної випадкової величи­ни Х задано таблицею:

	-4	-1
	0,1	0,2	0,1	0,3	0,1	0,2

Побудувати F(x) та її графік.

Розв'язання. Згідно з властивостями F(x), отримаємо наведені далі спiввiдношення,

1) ;

2) ;

3)

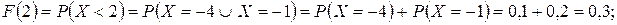
4)

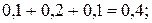
5)

6)

7)

=

=

+

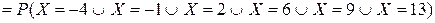Тоді F(x) можна записати в такій формі:

Графік функції F(x) зображено на рисунку 2.

 

 

Рисунок 2

Для неперервних випадкових величин закон розподілу ймовір­ностей зручно описувати з допомогою функції щiльностi ймовірностей, яку позначають f(х).

Щiльнiсmю ймовipностейнеперервної випадкової величини Х називається перша похідна від функції розподілу F(x):

, (7)

звідки .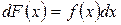

Оскільки

,

то добуток − ймовiрнiсть того, що випадкова величина Х мic­титиметься у проміжку , де . Функцію щільності розподілу називають ще диференціальною функцією розподілу.

Геометрично на графіку щiльностi ймовiрностi f(x)dx вiдповiдає площа прямокутника з основою dx i висотою f(x) (рисунок 3).

 

 

 

Рисунок 3

 

Наведемо властивості функції щільності f(x), які є наслідком її означення:

1. 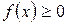. Ця властивість випливає з означення щільності ймовірності як першої похідної від за умови, що є неспадною функцією.

2. Площа, яку обмежує функція щільності розподілу та вісь , дорівнює 1:

. (8)

3. Наслідок із властивості (2): якщо неперервна випадкова величина Х визначена лише на проміжку 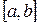, то

. (9)

4. Імовірність попадання неперервної випадкової величини в інтервал обчислюється за формулою

. (10)

5. Функція розподілу ймовірностей неперервної випадкової ве­личини має вигляд:

. (11)

Приклад 3: Закон неперервної випадкової величини Х зада­но у виглядi:

 

Знайти F(x) i по6удувати графiки функцiй f(х), F(x). 0бчислити .

Розв'язання.

1) для

;

2) для

= ;

3) для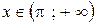

=

= .

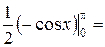
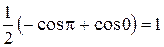Отже, функцiя розподiлу ймовiрностей буде така:

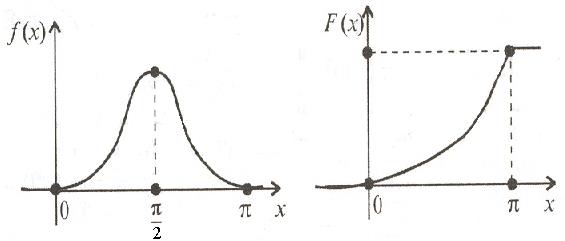Графiки функцiй f(х), F(x) зображенi вiдповiдно на рисунках 4 i 5.

 

Рисунок 4 Рисунок 5