Главная | Обратная связь

Випадкової величини

Приклад 8. Неперервна випадкова величина Х задана функцією щільності розподілу типу .

Необхідно знайти параметр С та інтегральну функцію . Побудувати графіки та . Обчислити числові характеристики , , , , .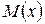

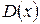Розв’язання: Для визначення параметра С використаємо властивість функції щільності розподілу (12): .

Врахуємо вигляд заданої функції і перепишемо це співвідношення з урахуванням властивостей визначених інтегралів:

,

,

 

,

 

,

,

,

,

.

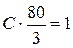Тоді має вигляд:

Згідно з визначенням функції розподілу маємо:

для : ;

для :

;

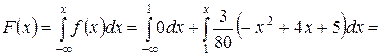
для :

Тоді

 

Знайдемо математичне сподівання та дисперсію:

 

.

Обчислимо

 

Тоді

.

Середнє квадратичне відхилення

.

Згідно з визначенням (15) мода є максимум функції щільності. Тоді обчислення моди − це є задача про пошук максимуму функції: за необхідною умовою існування екстремуму треба визначити похідну, прирівняти її до нуля, розв’язати рівняння, корені якого будуть точки підозрілі на екстремуми.

,

,

тоді,

,

,

.

− точка підозріла на екстремум. Враховуючи вигляд функції щільності, зокрема, це парабола, в якої гілки направлені вниз, можемо зробити висновок, що ця критична точка є максимумом функції, тобто .

Для обчислення медіани використаємо співвідношення . Зрозуміло, що , тоді

,

,

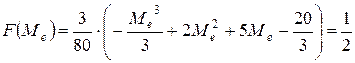або

.

Це рівняння можна розв’язувати наближено з використанням чисельних методів, наприклад, методу половинного ділення. При цьому слід врахувати, що . Для розв’язання рівняння можна використати стандартну функцію EXCEL − Подбор параметра. Тоді можна вважати в нашому випадку, що

.

За визначеними функціями щільності та розподілу побудуємо їх графіки. Обчислимо значення функцій у 10-12 точках, які належать заданому інтервалу. В перелік цих точок треба включити моду, математичне сподівання та медіану.

x
	0.3
1.5	0.328	0.158
	0.338	0.325
2.5	0.328	0.492
2.525	0.327	0.5
2.6	0.324	0.525
	0.300	0.650
3.5	0.253	0/789
	0.188	0.900
4.5	0.103	0.973

 

Графіки функцій та зображені на рисунках 13, 14.

Рисунок 13	Рисунок 14

 

 

ЗАДАЧІ

 

Неперервна випадкова величина Х задана функцією щільності розподілу типу .

Необхідно знайти параметр С та інтегральну функцію . Побудувати графіки та . Обчислити числові характеристики 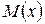, , 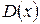, , 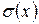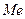. Вид функції та границі інтервалу наведені в таблиці.

 

№ варіанта		а	b
1.
2.
3.
4.
5.
6.
7.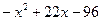
8.
9.
10.
11.
12.
13.		-4
14.
15.
16.
17.
18.
19.		-11
20.		-12
21.
22.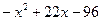
23.
24.
25.