 |
|
ВОПРОС 4 RSA АЛГОРИТМ
Обратные элементы в кольцах вычетов
Если же n _ простое, то согласно последнему свойству сравнения можно сокращать на любое ненулевое число. Более того, в кольце вычетов по простому модулю можно выполнять деление на любое ненулевое число и, как следствие, можно решать уравнения вида ax ≡ b (mod n). Решением такого уравнения явлется число x = ba−1, где a−1 _ обратный элемент к a в кольце вычетов по модулю n, то есть такое число, что aa−1 ≡ 1 (mod n). Если n _ простое, то для любого ненулевого числа существует обратный элемент, и, следовательно, можно делить на любое ненулевое число. Для нахождения обратного элемента к a в кольце вычетов по модулю n используем расширенный алгоритм Евклида для чисел a и n. Он найдет такие числа x и y, что ax + ny = 1, а, значит, ax ≡ 1 (mod n). Подумайте, для каких чисел a существует обратный элемент в кольце вычетов по модулю n, если n _ составное.
Шаг 1. Пусть d = (a, b, n) (наибольший общий делитель трех чисел).
Тогда сократим a, b, n на d (свойство 4).
Шаг 2. Если a необратим в кольце вычетов по модулю n, то решений
нет. Иначе x = ba−1 (mod n) _ решение.
Китайская теорема об остатках
В решении систем линейных сравнений помогает китайская теорема об остатках.Простейшая система сравнений имеет вид
x ≡ a (mod m),
x ≡ b (mod n),
где (m, n) = 1.
Тогда существует целое число c, такое, что эта система верна тогда, и только тогда, когда x ≡ c (mod mn).
Доказательство. Поскольку m и n _ взаимно простые, то существуют
числа r = n−1 (mod m) и s = m−1 (mod n). Положим c = arn + bsm.
Тогда если x ≡ c (mod mn), то
x ≡ c = arn + bsm ≡ arn ≡ ann−1 ≡ a (mod m)
x ≡ c = arn + bsm ≡ bsm ≡ bmm−1 ≡ b (mod n)
Докажем утверждение в другую сторону. Предположим, что x ≡ a
(mod m), x ≡ b (mod n). Выше было доказано, что c ≡ a (mod m) и
c ≡ b (mod n). Поэтому, x ≡ c (mod m), то есть x−c делится на m. Ана-
логично, x−c делится на n, откуда x−c делится на mn, следовательно,
x ≡ c (mod mn).
Подумайте сами, как быть с системой из трёх и более неравенств и
как быть, если m и n не взаимно просты.
Вопрос 2
идея алгоритма состоит в том, чтобы возвести a в произвольную степень, применяя элементарные операции возведения в квадрат и умножения. В качестве фазового пространства X этой задачи рассмотрим множество троек X = {(b,k,p)}. Здесь b выступает в роли текущего основания степени, k - в роли текущего показателя степени, p - это уже вычисленная часть степени. Ключевым моментом всегда является формулировка инварианта цикла:
I(b,k,p): bk*p = an = const, т.е. величина bk*p постоянна и равна an. Легко подобрать начальные значения так, чтобы инвариант выполнялся:
b0 = a; k0 = n; p0 = 1.
I(b0,k0,p0) = I(a,n,1): an*1 = an
Условие завершения совместно с выполнением инварианта должно обеспечить легкое решение требуемой задачи, т.е. вычисление an. Действительно, если k = 0, то из инварианта следует, что
b0*p = p = an, т.е. искомая величина содержится в переменной p. Итак, условие завершения состоит в равенстве нулю числа k:
Q(b,k,p): k = 0
Осталось написать преобразование T точки x = (b,k,p), которое сохраняет инвариант и одновременно уменьшает k. Определим преобразование T следующим образом:
T(b,k,p) = (b*b, k/2, p), если k четное
T(b,k,p) = (b, k-1, p*b), если k нечетное
Легко видеть, что инвариант сохраняется и k монотонно убывает. Итак, выпишем алгоритм быстрого возведения в степень для случая вещественного основания:
вещ алг. быстрое возведение в степень(вх: вещ a, цел n)
Вопрос 3
Определение группы
Пусть задано множество элементов G g1, g2, ... , gn , обладающих следующими свойствами:
1. Определен закон умножения элементов gi gj = gk, причем если gi, gj  G, то gi gj = gk
G, то gi gj = gk  G,
G,
i, j, l = 1, 2, ..., n.
2. Выполняется закон ассоциативности gi (gj gk) = (gi gj) gk.
3. Существует единичный элемент e, egi = gi, i = 1, 2, ... , n.
4. Существует обратный элемент g i-1, g i-1gi = e, i = 1, 2, ... , n.
Тогда на множестве G задана группа элементов g1, g2, ... , gn
ВОПРОС 4 RSA АЛГОРИТМ
Выберем группу 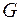 порядка
порядка 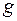 , который держится в секрете. Но при этом в группе
, который держится в секрете. Но при этом в группе 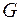 возможны вычисления. Пусть
возможны вычисления. Пусть  — обратимое целое число по модулю
— обратимое целое число по модулю 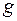 ,
, 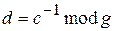 . Зашифруем элемент
. Зашифруем элемент  группы
группы 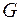 по правилу
по правилу  , а расшифруем по другому правилу
, а расшифруем по другому правилу 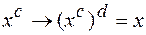 . При этом предполагается, что исходный текст можно разбить на части, которым можно взаимно однозначно сопоставить элементы группы
. При этом предполагается, что исходный текст можно разбить на части, которым можно взаимно однозначно сопоставить элементы группы 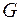 .
.
Пример. Пусть группа 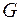 — мультипликативная группа вычетов по модулю
— мультипликативная группа вычетов по модулю 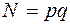 , где
, где  и
и  — различные простые числа, которые держатся в секрете. Порядок группы
— различные простые числа, которые держатся в секрете. Порядок группы 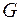 равен
равен  . В настоящее время считается, что задача разложения целого числа на простые множители настолько сложна, что это обеспечивает достаточную стойкость системы шифрования. Замечание 1. Свойство быть квадратичным вычетом сохраняется при зашифровке. Замечание 2. Неизвестно, является ли задача расшифровки в RSA алгоритме задачей, эквивалентной задаче факторизации целых чисел.
. В настоящее время считается, что задача разложения целого числа на простые множители настолько сложна, что это обеспечивает достаточную стойкость системы шифрования. Замечание 1. Свойство быть квадратичным вычетом сохраняется при зашифровке. Замечание 2. Неизвестно, является ли задача расшифровки в RSA алгоритме задачей, эквивалентной задаче факторизации целых чисел.
Замечание 3. Сравнение 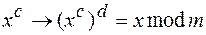 верно для любого класса вычетов по модулю
верно для любого класса вычетов по модулю  , а не только для вычетов взаимно простых с
, а не только для вычетов взаимно простых с  . Действительно, пусть
. Действительно, пусть  . Тогда
. Тогда  . Число
. Число  кратно
кратно  и значит
и значит  , следовательно,
, следовательно,  и так как
и так как  и
и  — различные простые числа, то
— различные простые числа, то 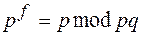 . Аналогично
. Аналогично 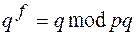 . Из мультипликативности классов вычетов следует, что сравнение верно для любого
. Из мультипликативности классов вычетов следует, что сравнение верно для любого  , так как любой необратимый элемент группы
, так как любой необратимый элемент группы 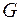 кратен
кратен  или
или  [ 5 ].
[ 5 ].
Пример (алгоритм RSA) . Пусть 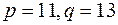 — простые числа,
— простые числа, 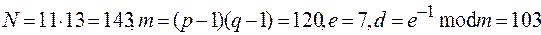 .Процесс шифрования выглядит так: :
.Процесс шифрования выглядит так: :  , т.е.
, т.е.  , а процесс расшифровки так :
, а процесс расшифровки так :  ,те
,те  .
.
Замечание. Допустим удалось получить тексты 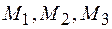 такие, что
такие, что 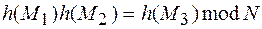 . Тогда, если
. Тогда, если  и
и  — законные подписи для текстов
— законные подписи для текстов  и
и  , то
, то  —законная подпись для текста
—законная подпись для текста  .
.