 |
|
Вопрос 6 АЛГОРИТМ ЭЛЕКТРОННОЙ ЦИФРОВОЙ ПОДПИСИ ЭЛЬ ГАМАЛЯ
Пусть 
— большое простое число, например, порядка 
, а 
— большое целое число, например, порядка 
, 
, оба числа не секретные, — образующая подгруппы простого порядка 
мультипликативной группы поля вычетов по модулю . Отправитель выбирает случайное число 
и вычисляет 
. Число 
передается всем корреспондентам для проверки подписи отправителя и по каким-то причинам они все знают, от кого оно получено (например, его роздал государственный центр по сертификации ключей ), число 
хранится отправителем в секрете.
Для получения цифровой подписи под сообщением 
необходимо выполнить следующие шаги:
Шаг 1 — вычислить хэш-код сообщения 
.
Шаг 2 — вычислить целое число 
, соответствующее вектору 
, и определить 
. Если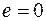 
, то определить 
.
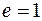Шаг 3 — сгенерировать псевдослучайное целое число 
, удовлетворяющее неравенству 
, и взаимно простое с 
.
Шаг 4 — вычислить значение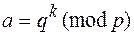 
и найти решение 
уравнения 
.
Пара чисел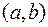 
и является цифровой подписью под данным сообщением.
Для проверки цифровой подписи 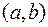под сообщением необходимо выполнить следующие шаги:
Шаг 1 — вычислить хэш-код сообщения .
Шаг 2 — вычислить целое число , соответствующее вектору , и определить . Если 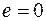, то определить .
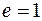Шаг 3 — вычислить число 
.
Шаг 4 — если выполнено равенство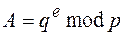 
, то подпись принимается, в противном случае подпись неверна.
Замечание. Если генератор случайных чисел генерирует мало чисел или их можно предсказать и какое-то число будет использовано дважды, то получим систему 
из которой можно найти секретный ключ .
Пример (алгоритм подписи Эль-Гамаля).
Пусть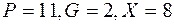 
. Тогда 
.
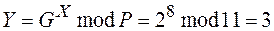Пусть далее 
, случайное 
, 
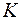и 
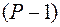взаимно просты. Тогда 
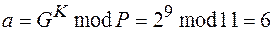. Решим теперь уравнение 
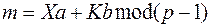. Получим 
, т.е.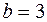 
.
Отправитель передает тройку 
.
Получатель находит 
и два числа 
и 
. Так как получились одинаковые значения, то сообщения признаются подлинными.
Замечание(обобщение системы Эль-Гамаля).
Алгоритм Эль-Гамаля обобщается следующим образом. Выбирают группу G , в которой легко вычисляется элемент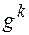 
, 
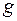— образующий элемент некоторой достаточно большой циклической группы известного порядка, но трудно решается задача дискретного логарифма, т.е. нахождения числа при известных 
такого, что 
. В качестве таких групп можно взять, например, мультипликативную группу вычетов по простому модулю, которая содержит циклическую подгруппу большого порядка или, скажем, циклическую подгруппу большого порядка группы точек эллиптической кривой над конечным полем.