 |
|
Вопрос 7 DSA (DIGITAL SIGNATURE ALGORITHM)
Алгоритм DSA был предложен в США для использования в стандарте цифровой подписи DSS (Digital Signature Standard). Стойкость ЭЦП основана на сложности вычисления дискретного логарифма в циклической группе простого конечного поля, а также на стойкости используемой в США хэш-функции .
Базовые математические объекты, используемые в процессах формирования и проверки ЭЦП алгоритма DSA, очень похожи на параметры отечественного стандарта.
Пусть  — простое число,
— простое число,  ,
,  — простое число,
— простое число,  и
и  является делителем для
является делителем для  ,
,  — целое число,
— целое число, 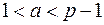 , при этом
, при этом  ,
,  — целое число,
— целое число,  . Пусть
. Пусть  — секретный ключ пользователя для формирования подписи,
— секретный ключ пользователя для формирования подписи, 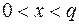 ,
,  — открытый ключ пользователя для проверки подписи,
— открытый ключ пользователя для проверки подписи,  .
.
Числа  не являются секретными. Конкретный набор их значений может быть общим для группы пользователей. Целое число
не являются секретными. Конкретный набор их значений может быть общим для группы пользователей. Целое число  , которое генерируется в процедуре подписи сообщения, должно быть секретным и должно быть уничтожено сразу после выработки подписи. Число
, которое генерируется в процедуре подписи сообщения, должно быть секретным и должно быть уничтожено сразу после выработки подписи. Число  снимается с физического датчика случайных чисел или вырабатывается псевдослучайным методом с использованием секретных параметров.
снимается с физического датчика случайных чисел или вырабатывается псевдослучайным методом с использованием секретных параметров.
Опишем теперь алгоритмы формирования и проверки цифровой подписи под сообщением пользователя.
Для получения цифровой подписи под сообщением  необходимо выполнить следующие шаги:
необходимо выполнить следующие шаги:
Шаг 1 — вычислить хэш-код сообщения  .
.
Шаг 2 — вычислить целое число  , соответствующее вектору
, соответствующее вектору  , и определить
, и определить  . Если
. Если 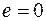 , то определить
, то определить 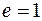 .
.
Шаг 3 — сгенерировать псевдослучайное целое число  , удовлетворяющее неравенству
, удовлетворяющее неравенству  .
.
Шаг 4 — вычислить два значения  и
и 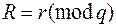 . Если
. Если  , то вернуться к шагу 3.
, то вернуться к шагу 3.
Шаг 5 — с использованием секретного ключа  отправителя сообщения вычислить значение
отправителя сообщения вычислить значение  . Если
. Если  , то вернуться к шагу 3.
, то вернуться к шагу 3.
Пара чисел 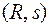 и является цифровой подписью под данным сообщением.
и является цифровой подписью под данным сообщением.
Для проверки цифровой подписи 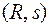 под сообщением
под сообщением  необходимо выполнить следующие шаги:
необходимо выполнить следующие шаги:
Шаг 1 — проверить выполнение неравенств 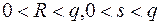 . Если неравенства выполняются, то перейти к следующему шагу. В противном случае подпись неверна.
. Если неравенства выполняются, то перейти к следующему шагу. В противном случае подпись неверна.
Шаг 2 — вычислить хэш-код сообщения  .
.
Шаг 3 — вычислить целое число  , соответствующее вектору
, соответствующее вектору  , и определить
, и определить  . Если
. Если 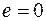 , то определить
, то определить 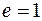 .
.
Шаг 4 — вычислить число 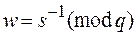 .
.
Шаг 5 — вычислить значения  и
и 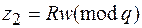 .
.
Шаг 6 — вычислить значение  .
.
Вопрос 8 ГОСТ Р 34.10 - 94).
Стойкость ЭЦП основана на сложности вычисления дискретного логарифма в циклической группе простого конечного поля, а также на стойкости используемой хэш-функции по ГОСТ Р 34.11.
Опишем базовые математические объекты, используемые в процессах формирования и проверки ЭЦП.
Пусть  — простое число,
— простое число,  либо
либо 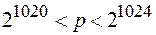 ,
,  — простое число,
— простое число,  и
и  является делителем для
является делителем для  ,
,  — целое число,
— целое число, 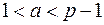 , при этом
, при этом  ,
,  — целое число,
— целое число,  .
.
Пусть  — секретный ключ пользователя для формирования подписи,
— секретный ключ пользователя для формирования подписи, 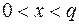 ,
,  — открытый ключ пользователя для проверки подписи,
— открытый ключ пользователя для проверки подписи,  .
.
Числа  не являются секретными. Конкретный набор их значений может быть общим для группы пользователей. Целое число
не являются секретными. Конкретный набор их значений может быть общим для группы пользователей. Целое число  , которое генерируется в процедуре подписи сообщения, должно быть секретным и должно быть уничтожено сразу после выработки подписи. Число
, которое генерируется в процедуре подписи сообщения, должно быть секретным и должно быть уничтожено сразу после выработки подписи. Число  снимается с физического датчика случайных чисел или вырабатывается псевдослучайным методом с использованием секретных параметров.
снимается с физического датчика случайных чисел или вырабатывается псевдослучайным методом с использованием секретных параметров.
Опишем теперь алгоритмы формирования и проверки цифровой подписи под сообщением пользователя.
Для получения цифровой подписи под сообщением  необходимо выполнить следующие шаги:
необходимо выполнить следующие шаги:
Шаг 1 — вычислить хэш-код сообщения  .
.
Шаг 2 — вычислить целое число  , соответствующее вектору
, соответствующее вектору  , и определить
, и определить  . Если
. Если 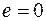 , то определить
, то определить 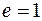 .
.
Шаг 3 — сгенерировать псевдослучайное целое число  , удовлетворяющее неравенству
, удовлетворяющее неравенству  .
.
Шаг 4 — вычислить два значения  и
и 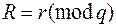 . Если
. Если  , то вернуться к шагу 3.
, то вернуться к шагу 3.
Шаг 5 — с использованием секретного ключа  пользователя (отправителя сообщения) вычислить значение
пользователя (отправителя сообщения) вычислить значение  . Если
. Если  , то вернуться к шагу 3.
, то вернуться к шагу 3.
Пара чисел 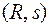 и является цифровой подписью под данным сообщением.
и является цифровой подписью под данным сообщением.
Для проверки цифровой подписи 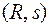 под сообщением
под сообщением  необходимо выполнить следующие шаги:
необходимо выполнить следующие шаги:
Шаг 1 — проверить выполнение неравенств 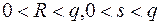 . Если неравенства выполняются, то перейти к следующему шагу. В противном случае подпись неверна.
. Если неравенства выполняются, то перейти к следующему шагу. В противном случае подпись неверна.
Шаг 2 — вычислить хэш-код сообщения  .
.
Шаг 3 — вычислить целое число  , соответствующее вектору
, соответствующее вектору  , и определить
, и определить  . Если
. Если 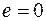 , то определить
, то определить 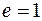 .
.
Шаг 4 — вычислить число 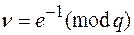 .
.
Шаг 5 — вычислить значения  и
и 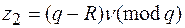 .
.
Шаг 6 — вычислить значение  .
.
Шаг 7 — если выполнено равенство  , то подпись принимается в противном случае подпись неверна.
, то подпись принимается в противном случае подпись неверна.
Замечание. Важным моментом является получение чисел  , удовлетворяющих перечисленным требованиям.
, удовлетворяющих перечисленным требованиям.