 |
|
Вопрос 13 РАЗДЕЛЕНИЕ СЕКРЕТА
Пусть имеются два владельца сейфа и дилер, которому они оба доверяют. Код сейфа является 16-значным числом. Дилер должен сообщить каждому владельцу его часть кода так, чтобы они могли открыть его вдвоем, но не могли это сделать порознь. Если, например, дилер сообщает первому первые 8 цифр, а второму — вторые 8 цифр, то каждому из них для взлома придется перебрать не более 
вариантов. Гораздо эффективнее другой способ разделения секрета. Дилер выбирает два ключа из 16 цифр каждый и втайне сообщает каждому владельцу свой ключ, а сам складывает соответствующие цифры ключей по модулю 10 и закрывает сейф с помощью полученного ключа. Теперь для взлома необходимо перебрать уже 
вариантов.
Более интересна схема разделения секрета между N участниками так , чтобы любые K+1 участников могли восстановить секрет, но при этом никакие K участников не могли бы этого сделать.
Итак, пусть в протоколе разделения секрета имеется N участников 
и дилер D. Протоколы состоят из двух фаз: фазы разделения секрета и фазы восстановления секрета. На первой фазе дилер генерирует N долей секрета 
и по защищенным каналам посылает долю секрета 
участнику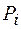 
. На фазе восстановления секрета любое подмножество из не менее чем K+1 участника однозначно восстанавливает секрет, обмениваясь сообщениями по защищенным каналам. А любое подмножество из не более чем K участников не может восстановить секрет. Неплохо было бы, если бы каждый участник 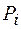мог проверить, что его доля секрета действительно есть доля секрета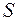 
. Это позволит проверить, что другой участник не пытается подсунуть ему фикцию при восстановлении секрета.
Рассмотрим одну конструкцию проверяемого разделения секрета на основе дискретного логарифма. Пусть 
и 
— простые, делит 
, 
. Дилер выбирает случайный полином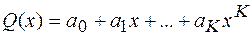 
, где 
— секрет, вычисляет числа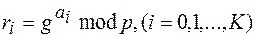 
и публикует 
. Затем дилер вычисляет числа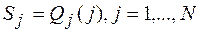 
и посылает их соответствующим участникам 
по защищенным каналам.
Участник вычисляет 
и убеждается, что 
— доля секрета 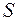, так как 
.
Для фазы восстановления считаем, что дилер — честный.
Всякий участник (честный) посылает каждому другому участнику 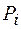свою долю секрета . Всякий честный участник 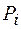может проверить, что прислал правдивую информацию. Так как честных участников не менее чем K+1, то каждый из них будет иметь не менее чем K+1 правильную долю секрета.
Имея K+1 узел 
, для полинома степени K можно построить интерполяционный многочлен Лагранжа и найти затем секрет 
. Если знать меньше узлов чем K , то найти однозначно коэффициент полинома 
невозможно.
Вопрос 14