 |
|
Элементы теории четырехполюсников
Четырехполюсниками называют цепи, взаимодействующие с другими цепями посредством двух пар зажимов (полюсов).
Методы теории четырехполюсников применяют для упрощения анализа сложных цепей, а также для анализа устройств, внутреннее строение которых неизвестно. В этом случае четырехполюсники моделируют некоторые процессы, являясь «черным ящиком», связанным с внешним миром посредством четырех полюсов (зажимов). Так, например, в радиотехнике моделируют процессы в электронных лампах и транзисторах.
Электрическое состояние четырехполюсника однозначно и полностью описывается четырьмя величинами: входными напряжением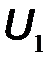 
и током 
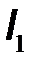и выходными напряжением 
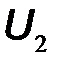и током 
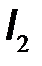. Направление отсчетов мгновенных значений напряжений и токов выберем, как указано на рис. 2.10.
Рис. 2.10. Направление отсчетов мгновенных значений напряжений и токов на зажимах четырехполюсника
Из четырех величин 
, 
, 
, 
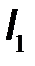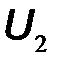две могут рассматриваться как заданные, являясь воздействиями, аргументами, а две другие – как их функции, отклики. Существует шесть вариантов такого представления, определяя шесть разновидностей систем уравнений второго порядка, описывающих электрическое состояние четырехполюсника в тех или иных параметрах. Рассмотрим те из них, которые наиболее широко используются в радиоэлектронике.
1.Система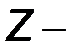 
параметров. Для определения 
параметров четырехполюсника в качестве аргументов используют токи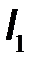 
, 
, а в качестве функций – напряжения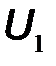 
, 
: на основании второго закона Кирхгофа записывают систему уравнений
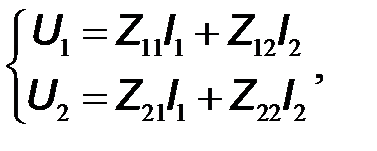(2.22)
которая в матричной форме имеет вид:
(2.23)
Размерность 
параметров – размерность сопротивления, Ом.
Для определения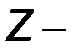 
параметров и выяснения их физического смысла применим процедуру мысленного размыкания одной из пар зажимов четырехполюсника, определяя 
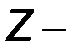параметры в режиме холостого хода, когда или 
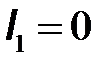или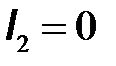 
.
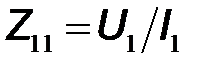– входное сопротивление в режиме холостого хода выхода;
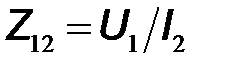– взаимное сопротивление обратной передачи с выхода на вход в режиме холостого хода входа;
– взаимное сопротивление прямой передачи в режиме холостого хода выхода;
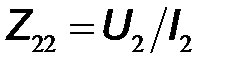– выходное сопротивление в режиме холостого хода входа.
2.Система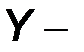 
параметров. В этом случае в качестве аргументов используются напряжения 
, 
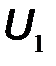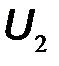, а в качестве функций – токи 
, 
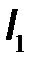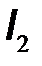. На основании первого закона Кирхгофа записываем систему уравнений
(2.24)
которая в матричной форме имеет вид:
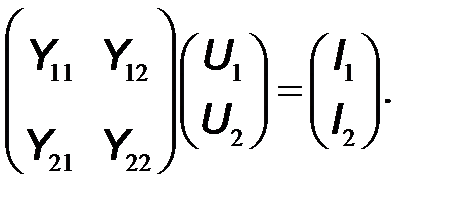(2.25)
Размерность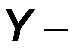 
параметров – размерность проводимости, См.
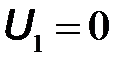параметры четырехполюсника и их физический смысл определяются в режиме короткого замыкания, когда или 
, или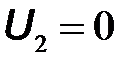 
.
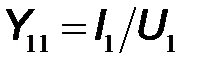– входная проводимость при короткозамкнутом выходе;
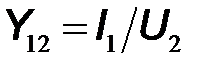– взаимная проводимость обратной передачи при короткозамкнутом входе;
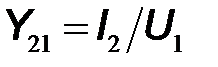– взаимная проводимость прямой передачи в режиме короткого замыкания выхода;
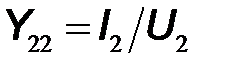– выходная проводимость в режиме короткого замыкания входа.
3. Система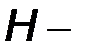 
параметров. При определении гибридных 
параметров в качестве аргументов используются входной ток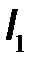 
и выходное напряжение 
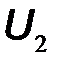, а в качестве функций – входное напряжение 
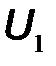и выходной ток 
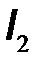. Система уравнений имеет следующий вид:
(2.26)
В матричной форме (2.26) имеет вид:
(2.27)
Гибридные коэффициенты определяются в разных режимах.
– входное сопротивление в режиме короткого замыкания выхода;
– безразмерный коэффициент обратной передачи напряжения в режиме холостого хода входа;
– безразмерный коэффициент прямой передачи тока в режиме короткого замыкания выхода;
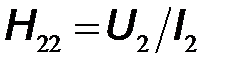– выходная проводимость в режиме холостого хода входа.
Для примера на рис. 2.11 приведена формальная эквивалентная схема замещения четырехполюсника в системе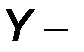 
параметров.
Исторически сложилось так, что в радиотехнических справочниках характеристики электронных ламп и полевых транзисторов приводятся в системе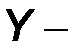 
параметров, а характеристики биполярных транзисторов – в системе 
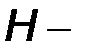параметров. В дальнейшем при анализе схем на электронных приборах, работающих в линейном режиме, будем пользоваться формальной эквивалентной схемой замещения в системе 
параметров.
Рис. 2.11. Формальная эквивалентная схема замещения четырехполюсника в системе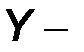 
параметров