 |
|
Основы метода комплексных амплитуд
Гармоническому колебанию какой-либо физической величины
(2.7)
сопоставляется комплексное представление
. (2.8)
Здесь: 
– сомножитель, описывающий временную зависимость; 
– мнимая единица; 
– комплексная величина, называемая комплексной амплитудой соответствующей физической величины. Модуль комплексной амплитуды 
определяет амплитуду исходного колебания, а аргумент 
– начальную фазу.
В теории цепей гармоническим колебаниям напряжения и тока сопоставляются комплексы:
, (2.9)
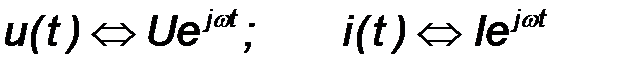, (2.15)
где 
и 
– комплексные амплитуды напряжения и тока. В конкретных цепях 
и 
являются искомыми переменными в уравнениях электрического равновесия. Решение этих уравнений в комплексной форме определяет амплитуды и начальные фазы изначально искомых напряжений и токов: 
, 
; 
, 
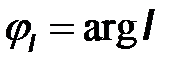. Формально переход от комплексных амплитуд к мгновенным значениям напряжений и токов осуществляется посредством формулы:
. (2.10)
Представленные выше исходные понятия теории электрических цепей в комплексной форме принимают вид, приведенный в таблице 2.2.
Важным свойством метода комплексных амплитуд является то, что операциям дифференцирования и интегрирования соответствуют умножение и деление на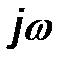 
. Это приводит к тому, что, например, электрическое состояние цепи, приведенной на рис. 2.6, методом комплексных амплитуд будет представлено не интегро-дифференциальным уравнением (2.6), а линейным алгебраическим уравнением
, (2.6а)
решение которого, с учетом формулы (2.10), легко находится.
Таким образом, применение метода комплексных амплитуд существенно упрощает получение результатов при анализе гармонических колебаний в линейных физических системах. Его положительным качеством также является наглядность представления гармонических процессов посредством векторных диаграмм на комплексной плоскости.
Таблица 2.2
Основные понятия теории электрических цепей в комплексной форме
| Напряжение | | 
| |
| Ток | | 
| |
| Источник напряжения | | 
| (2.11) |
| Источник тока | | 
| (2.12) |
| Резистивность | | 
| (2.13) |
| Емкость | | 
| (2.14) |
| Индуктивность | | 
| (2.15) |
| Первый закон Кирхгофа | | 
| (2.16) |
| Второй закон Кирхгофа | | 
| (2.17) |