 |
|
Тема 2 Статистика выводов
- Нормальное распределение. Центральная предельная теорема .
- Распределения Стьюдента и Фишера
- Доверительный интервал.
- Проверка статистических гипотез (Критерии Стьюдента, Фищера)
- Нормальное распределение. Центральная предельная теорема
Нормальное распределение - является наиболее важным распределением статистического анализа. Многие случайные переменные удовлетворяют нормальному распределению, а во многих статистических тестах предполагается, что данные удовлетворяют нормальному распределению. Разнообразные статистические данные с хорошей степенью точности можно считать реализациями случайной величины, имеющей нормальное распределение. Можно предполагать нормальное распределение у случайной величины, если на её отклонение от некоторого фиксированного значения аддитивно влияет множество различных факторов, причем влияние каждого из них вносит малый вклад в это отклонение, а их действия почти независимы. Кроме того, в силу центральной предельной теоремы распределение целого ряда широко распространенных в статистике функций от случайных величин хорошо аппроксимируется нормальным распределением. Нормальное распределение часто встречается в реальных исследованиях. Оно удобно для компьютерной обработки. Использованию нормального распределения для приближенного описания случайных величин не препятствует то обстоятельство, что эти величины обычно могут принимать значения только из какого-то ограниченного интервала (скажем, размер изделия должен быть больше нуля и меньше километра), а нормальное распределение не сосредоточено целиком ни на каком интервале. Однако, вероятность больших отклонений нормальной случайной величины от среднего значения настолько мала, что ее практически можно считать равной нулю. Кроме того, линейная комбинация любых нормально распределённых величин вновь распределена нормально.
Для исследования "нормальных" данных математической статистикой выработаны эффективные методы. Эти методы непригодны для данных другой природы в том смысле, что выполнить соответствующий расчёт можно, но результат будет неправильным. Поэтому, когда к имеющимся наблюдениям применяются ориентированные на нормальное распределение методы, необходимо выяснить, похоже ли распределение этих наблюдений на нормальное. С полной уверенностью сказать это невозможно, но, по крайней мере, от грубых ошибок такие проверки могут уберечь.
Случайная величина ξ имеет нормальное распределение вероятностей с параметрами а и σ² (обозначение: ξ ~ N(a, σ²)), если ее плотность распределения задается формулой:
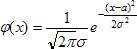
Математическое ожидание и дисперсия случайной величины ξ ~ N(a, σ²) равны Е(ξ) = a,
(ξ) = σ². Другими словами случайная величина группируется вблизи a, причем типичные отклонения от a близки к σ (σ > 0). Плотность распределения стремится к нулю при удалении х от среднего значения. График функции плотности симметричен относительно точки а. Значит, медиана нормального распределения равна а. В точке а функция φ(х) достигает своего максимума, который равен 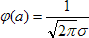 . Значит, мода нормального распределения равна а. Таким образом, параметр а характеризует положение графика функции на числовой оси. Это параметр положения. Параметр σ характеризует степень сжатия или растяжения графика плотности. Это параметр масштаба. Вся совокупность нормальных распределений представляет собой двухпараметрическое семейство. Рассмотрим случайную величину η ~ N(0, 1). Случайная величина:
. Значит, мода нормального распределения равна а. Таким образом, параметр а характеризует положение графика функции на числовой оси. Это параметр положения. Параметр σ характеризует степень сжатия или растяжения графика плотности. Это параметр масштаба. Вся совокупность нормальных распределений представляет собой двухпараметрическое семейство. Рассмотрим случайную величину η ~ N(0, 1). Случайная величина:

Следовательно, характеристики любой нормально распределённой случайной величины легко определить по соответствующим характеристиками стандартной нормально распределённой величины с параметрами а = 0 и σ = 1. Плотность стандартного нормального распределения есть 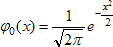 . Функция распределения стандартного нормального распределения обозначается Ф(х) и её часто называют функцией Лапласа. Функция произвольного нормального распределения N(a, σ²):
. Функция распределения стандартного нормального распределения обозначается Ф(х) и её часто называют функцией Лапласа. Функция произвольного нормального распределения N(a, σ²):
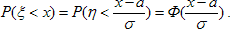
Известно, что площадь фигуры, ограниченная графиком функции плотности распределения, осью абсцисс и отрезками двух вертикальных прямых, х = b, х = с, есть вероятность попадания случайной величины в интервал (b, с). В связи с этим полезно знать, как распределяются доли площадей между кривой φ(х) и осью абсцисс. Случайная величина N(0,1) с вероятностью, примерно равной 34,1% попадает в интервал (0;1), с вероятностью 13,6% попадает в интервал (1;2), с вероятностью, примерно равной 2,14% попадает в интервал (2;3), с вероятностью, примерно равной 0,13% попадает в интервал (3;4). Отсюда для произвольной нормально распределенной случайной величины можно сформулировать правило, именуемое в литературе правилом сигм: нормально распределённая случайная величина ξ ~ N(a, σ²) как правило, попадает в интервал (а - 2σ, а + 2σ) (с вероятностью 95,44%), и практически наверняка попадает в интервал (а - 3σ, а + 3σ) (вероятность 99,73%). Верхние односторонние квантили распределения имеют следующий смысл. Высказывание "верхняя 95%-ая односторонняя квантиль равна 1,64" означает, что с вероятностью 95% стандартная нормально распределённая случайная величина не превышает 1,64. При этом Ф(1,64) ≈ 0,95. Односторонние квантили таковы:
95% - 1,64; 97,5% - 1,96; 99% - 2,33; 99,5% - 2.58.
Верхние двусторонние квантили распределения имеют следующий смысл. Высказывание "верхняя 95%-ая двусторонняя квантиль равна 1,96, означает, что с вероятностью 95% стандартная нормально распределённая случайная величина по модулю не превышает 1,96. Ясно, что односторонняя (1 - ε) квантиль совпадает с двусторонней (1 - 2ε) квантилью. Двусторонние квантили таковы:
95% - 1,96; 97,5% - 2,24; 99% - 2,58; 99,5% - 2.81.
Если ξ1 и ξ2 - независимые нормально распределенные случайные величины с параметрами a1, σ1² и a2, σ2² соответственно, то их сумма ξ1 + ξ2 тоже распределена по нормальному закону, притом с параметрами a1 + a2 и σ1² + σ2².
Для окончательной проверки закона распределения наблюдений используют критерии согласия. Однако в качестве первого шага проверки удобно применять простой
Распределение выборочных средних для случайных выборок данных, каждый элемент которых подчиняется нормальному распределению со средним 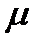 и стандартным отклонением
и стандартным отклонением  также будет нормальным со средним а и стандартным отклонением
также будет нормальным со средним а и стандартным отклонением 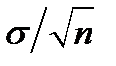 , где
, где 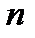 — размер выборки. Например, если каждое наблюдение подчиняется нормальному распределению со средним 0 и стандартным отклонением 1, то выборочное среднее для выборки из 100 таких наблюдений также будет нормальным со средним 0 и стандартным отклонением 0,1.
— размер выборки. Например, если каждое наблюдение подчиняется нормальному распределению со средним 0 и стандартным отклонением 1, то выборочное среднее для выборки из 100 таких наблюдений также будет нормальным со средним 0 и стандартным отклонением 0,1.
Увеличивая размер выборки, можно наблюдать визуальное представление зависимости между размером выборки и выборочным стандартным отклонением. Обратите внимание: при увеличении размера выборки диапазон наиболее вероятных значений сужается и приближается к значению 0, т.е. более крупные выборки позволяют точнее оценивать выборочное среднее