Главная | Обратная связь

Постановка задачи линейного программирования (ЗЛП)

 

В задаче ЛП целевая функция представляет собой линейную форму вида

F= С₁Х₁ + С₂Х₂ +... + С_пХ_п, (3.1)

а система ограничений на переменные - систему линейных уравнений и неравенств

(3.2)

 

x_j>=0 (j=1,2,...,n) (3.3)

Каждое решение системы (3.2)-(3.3) представляет собой совокупность значений переменных Х₁, Х₂,...,Х_n, удовлетворяющих всем неравенствам системы. Эту совокупность можно рассматривать как точку или вектор в n -мерном векторном пространстве.

Задача линейного программирования может быть представлена:

1) в векторном виде

F=CX,

A₁X₁+A₂X₂+...+A_nX_n= В ,

X>=0,

где С = (с₁, с₂,..., с_n); X = (х₁, х₂,..., х_n); CX— скалярное произведение;

векторы

, , …, ,

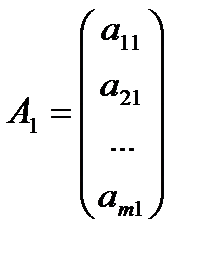состоят соответственно из коэффициентов при неизвестных и свободных членах;

2) в матричном виде

F = СХ,

АХ = В,

Х>=0.

3) с помощью знаков суммирования

F= å с_j x_j i = 1.m,

^jÎJ

е a_ij x_j =b_i j = 1.п ,

^{jÎ J}

х_j >= 0.

Существующие методы решения задач линейного программирования (ЗЛП) во многом определяются видами ограничений. В связи с этим различают задачи линейного программирования в общем виде, в канонической и стандартной (симметрической) формах:

1) в общем виде

F= å с_j x_j min (max)

^jÎJ

при условиях: _>=

е a_ij x_j { = } b_i i=1.m,

^{jÎ J <=}

x_j>=0 j=1.n,

2)в канонической форме

F= å с_j x_j min (max)

^jÎJ

при условиях: е a_ij x_j =b_i i = 1.m,

^{jÎ J}

x_j>=0 j =1.n

3) в стандартной (симметрической) форме

 

F(min(max)) = å с_j x_j

^jÎJ

при условиях: е a_ij x_j >= b_i ,

^{jÎ J}

е a_ij x_j <= b_i , i =1.m,

^{jÎ J}

x_j >=0 , j= 1.n

Все три формы задач ЛП эквивалентны и легко переводятся из одной в другую. Для перехода от общей или стандартной формы к канонической нужно в каждое ограничение-неравенство ввести свою дополнительную переменную с коэффициентом (+1), если неравенство типа «<=», и с коэффициентом (-1), если неравенство типа «>=». Дополнительные переменные должны удовлетворить условию неотрицательности и входить в целевую функцию с нулевыми коэффициентами.

Введем некоторые определения.

Определение 1. Совокупность значений переменных Х = (х₁, х₂, . . . х_п),удовлетворяющих всем неравенствам системы (3.2) называется решением.

Определение 2 Решение Х = (х₁, х₂, ... х_п), удовлетворяющее условиям неотрицательности (3.3) называется допустимым решением ЗЛП.

Определение 3. Допустимое решение Х = (х₁, х₂, ... х_п)называется опорным (базисным), если векторы А_i входящие в разложение

А₁X₁+A₂X₂+ ... + A_nX_n = Вc положительными коэффициентами Х_j, являются линейно независимыми.

Векторы А_i являются m - мерными, а из определения опорного плана следует, что число его положительных компонент не может превышать m.

Определение 4. Оптимальным решением задачи ЛП (3.1)-(3.3) называется допустимое решение, обеспечивающее экстремальное значение линейной функции.