 |
|
Центрально предельная теорема (теорема Чебышева- Ляпунова)
Если каждое наблюдение подчиняется распределению со средним а и стандартным отклонением 
, то, согласно центральной предельной теореме, распределение выборочных средних приблизительно удовлетворяет нормальному распределению со средним а и стандартным отклонением 
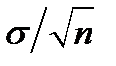, где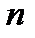 
— размер выборки. Эта теорема справедлива для любого распределения, если его среднее и стандартное отклонение существуют и имеют конечные значения. Например, распределение выборочных средних для случайных выборок из данных, которые подчиняются равномерному распределению, приблизительно удовлетворяет нормальному распределению (а не равномерному распределению, как можно было бы ожидать). Чем больше размер выборки, тем точнее распределение выборочных средних удовлетворяет нормальному распределению.
- Распределения Стьюдента и Фишера
Чтобы использовать нормальное распределение для анализа данных, нужно точно знать значение 
, что не всегда возможно и потому приходится использовать оценку . В таких случаях вместо нормального распределения следует использовать t-распределение. Оно характеризуется параметром, который влияет на точность оценки , а именно степенями свободы. При анализе выборочных данных количество степеней свободы равняется количеству наблюдений минус 1.
По мере увеличения количества степеней свободы (т.е. возрастания размера выборки) t-распределение точнее соответствует нормальному распределению. При этом оценка также становится точнее. Для низкого количества степеней свободы t-распределение имеет более длинные хвосты, чем нормальное распределение. При ошибочном использовании нормального распределения вместо t-распределения возможна недооценка вероятностей экстремальных значений. Для определения вероятности распределения по заданного х для можно использовать функцию Excel - СТЬЮДРАСП (x; степени_свободы; хвосты),где x — численное значение, для которого требуется вычислить распределение; степени_свободы — целое, указывающее число степеней свободы, хвосты — число возвращаемых хвостов распределения. Если хвосты = 1, то функцияСТЬЮДРАСП возвращает одностороннее распределение. Если хвосты = 2, то функция СТЬЮДРАСП возвращает двухстороннее распределение. Вместо таблицы для определения критических значений t-распределения при проверки гипотез по критерию Стьюдента можно использовать функцию Excel - СТЬЮДРАСПОБР (вероятность; степени_свободы),где вероятность – вероятность, связанная с t – распределением.
F-распределение Фишера используется преимущественно для статистического анализа регрессии и дисперсии данных. F-распределение характеризуется двумя параметрами степени свободы: числителем и знаменателем степеней свободы. Эти параметры используются для вычисления среднеквадратической ошибки разных факторов регрессии и дисперсии данных. F-распределение часто обозначается как 
, где 
— числитель, а 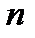— знаменатель степеней свободы. В Excel имеется две функции, связанные с F – распределением:
- FРАСП(х, степень свободы1, степень свободы2) -где x — численное значение, для которого требуется вычислить распределение; степенъ_свободы1 — целое, указывающее число степеней свободы числителя,степенъ_свободы2 - целое, указывающее число степеней свободы знаменателя.
- FРАСПОБР(вероятность, степень свободы1, степень свободы2) -где вероятность – вероятность, связанная с F – распределением. Данная функция может быть использована вместо таблицы для определения критического значения F – критерия при проверке гипотез по критерию Фишера.
- Доверительный интервал
Доверительным интервалом называется интервал, содержащий истинное значение параметра с заданной вероятностью Р.
Для оценки грубого доверительного интервала используются два утверждения.
1. Выборочное среднее удовлетворяет нормальному распределению со средним 
и стандартным отклонением 
.
2. В нормальном распределении около 95% значений попадают в диапазон ±2 стандартных отклонения от среднего .
Это значит, что выборочное среднее попадает в диапазон ±2 стандартных отклонения в 95% случаев. Например, если 
, то выборочное среднее 50 для 25 наблюдений будет иметь стандартную ошибку 0,8 и можно на 95% быть уверенным в том, что истинное значение находится в пределах 50±2*0,8=50±1,6. Таким образом, можно с 95%-ной уверенностью утверждать, что истинное значение находится в диапазоне от 48,4 до 51,6. Для уменьшения доверительного интервала можно просто увеличить размер выборки. Если вместо выборки из 25 наблюдений используется выборка из 100 наблюдений, то доверительный интервал будет равен (49,2; 50,8).
Для получения более точной меры доверительного интервала нужно использовать z-значения. 
- это точка на кривой стандартного нормального распределения, для которой вероятность нахождения меньшего или равного значения равна 
. Например, 
= 1,645, т.е. 95% всех значений стандартного нормального распределения меньше или равны 1,645. z-значения используются в тех случаях, когда задана вероятность встретить значение, меньшее или равное z-значению.
Если нужно найти диапазон значений в центральной части распределения с заданной вероятностью, (например, требуется найти диапазон значений в центральной части стандартного нормального распределения с вероятностью 95%), то вводится параметр 
(вероятность встретить наблюдение за пределами центральной части) и вычисляются следующие значения: 
Иначе говоря, 95% всех значений стандартного нормального распределения лежат в промежутке между –1,96 и 1,96 (что близко использованной ранее грубой оценке ±2)
Степень приближения выборочного распределения к нормальному распределению зависит от размера выборки и распределения вероятностей для отдельных наблюдений. Для больших выборок приближение к нормальному распределению может быть очень точным, а для маленьких выборок — менее точным. Если исходное распределение вероятностей очень скошено, то потребуется выборка гораздо большего размера для более точного приближения к нормальному распределению.
Насколько большой должна быть выборка? Если исходное распределение не очень скошено, то достаточно 20–30 наблюдений Ключевым параметром оценки точности выборочного среднего является стандартная ошибка. Это мера точности выборочного среднего, она равна , где 
— стандартное отклонение плотности вероятности; 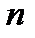— размер выборки. Например, выборочное среднее для 25 наблюдений, удовлетворяющих нормальному распределению, с 
имеет стандартную ошибку 
. Выборочное среднее удовлетворяет нормальному распределению со средним, равным , и стандартным отклонением, равным стандартной ошибке. Таким образом, если выборочное среднее вычислено для выборки из 25 наблюдений, то оно удовлетворяет нормальному распределению со средним, равным , и стандартным отклонением, равным 0,8. С помощью z-значений можно точнее оценить доверительный интервал и определить общую форму доверительного интервала. Точная формулировка доверительного интервала для выборочного среднего имеет следующий вид:
.
Таким образом, для случайной выборки 25 наблюдений, удовлетворяющих нормальному распределению, с 
доверительный интервал выборочного среднего имеет следующий вид:
Таким образом, на 95% можно быть уверенным, что значение 
лежит в пределах ±1,568 единицы от выборочного среднего. С помощью такого же метода можно определить, что 99%-ный доверительный интервал лежит в пределах ±2,0608 единицы от выборочного среднего.