Главная | Обратная связь

Основы теории колебаний

 

Процессы, характеризующиеся повторяемостью во времени, называются колебательными. При периодических колебаниях величина, определяющая состояние системы, повторяется через равные промежутки времени – период колебания T. Частота колебания n – величина обратная периоду, она равна количеству колебаний, совершаемых за единицу времени:

 

.

Вид зависимости колеблющейся величины от времени определяет форму колебания. Наиболее важны гармонические колебания, в которых переменная величина x изменяется по закону синуса или косинуса (рис. 2.1). Такие колебания достаточно часто встречаются в природе, а колебания более сложной формы всегда можно представить как суперпозицию простых гармонических колебаний.

 

Рис. 2.1. Гармоническое колебание x(t)

 

Закон гармонических колебаний можно записать в виде

 

,

(2.1)

 

гдеA – амплитуда колебания; w - циклическая частота; j₀ – начальная фаза.

Значение колеблющейся величины в данный момент времени t определяется значением фазы колебания . Быстрота изменения фазы характеризуется величиной w – циклической частотой колебаний, которая равна числу колебаний за 2p секунд:

 

.

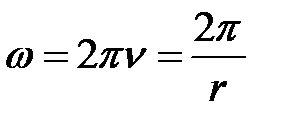Величина j₀– значение фазы колебания в начальный момент времени t = 0.

Рассмотрим движение материальной точки, совершающей гармонические колебания вдоль оси Оx: , где x – отклонение материальной точки от положения равновесия, принятого за ноль координатной оси Ox. Система, имеющая такой закон движения, называется одномерным гармоническим осциллятором. Модуль наибольшего отклонения системы от положения равновесия называется амплитудой колебания: А= x_max.

При гармонических колебаниях и скорость, и ускорение осциллятора изменяются со временем по гармоническому закону с той же частотой, но со сдвигом по фазе. Для проекций векторов скорости и ускорения на ось Оx:

;

.

Видно, что a_x = x² = -w²x, следовательно,

 

x² +w2x = 0.

(2.2)

 

Это уравнение называется уравнением гармонического осциллятора, его решением является функция, описывающая изменение величины x со временем по гармоническому закону (2.1).

Определим по второму закону Ньютона проекцию силы F_x, действующей на материальную точку массой m, совершающую гармоническое колебание с ускорением a_x:

 

F_x = ma_x = -mw²x = -kx,

 

где k = mw².

Сила, под действием которой совершаются гармонические колебания, пропорциональна смещению и направлена к положению равновесия. В соответствии с законом Гука это справедливо для силы упругости, причем k – коэффициент упругости. Силы вида F_x = -kx, независимо от их природы, называются квазиупругими, их действие приводит к возникновению механических гармонических колебаний. Квазиупругие силы возникают при малых смещениях тела от положения равновесия.

Колебания в системе, выведенной из положения равновесия и предоставленной самой себе, называются свободными. Если силой трения можно пренебречь, движение происходит под действием квазиупругой силы. Частота свободных колебаний определяется свойствами самой колеблющейся системы и называется собственной частотой системы . Отсюда период собственных колебаний

.

 

а б

 

Рис. 2.2. Физический (а) и математический (б) маятники

 

Рассмотрим в качестве примеров гармонических осцилляторов физический и математический маятники, совершающие малые колебания под действием силы тяжести. Физический маятник (рис. 2.2, а) – это твердое тело, колеблющееся на закрепленной горизонтальной оси, не проходящей через его центр тяжести. Математический маятник (рис. 2.2, б) – материальная точка, подвешенная на невесомой, нерастяжимой нити, является частным случаем физического. При отклонении маятника от положения равновесия на угол a возникает вращающий момент силы тяжести M, сообщающий ему угловое ускорение e = a², которое может быть определено из основного закона динамики вращательного движения: , где I – момент инерции маятника относительно оси О. Если расстояние от оси О до центра тяжести маятника – l ,то момент силы тяжести относительно этой оси в данный момент колебаний . Знак минус показывает, что сила тяжести mg стремится вернуть маятник в равновесное положение. При малых отклонениях от положения равновесия (a < 6°) справедливо: и .Подставив это выражение в основной закон динамики, получим: , откуда , или

 

.

(2.3)

 

Сравнив равенства (2.3) и (2.2), видим, что это уравнение гармонического осциллятора, совершающего свободные незатухающие колебания с циклической частотой

.

Соответственно, период малых колебаний маятника не зависит от их амплитуды и определяется его геометрией

 

.

Для математического маятника длиной l и массой m момент инерции относительно оси О найдем как момент инерции материальной точки: I = ml². Тогда для периода колебаний математического маятника получим

 

.

(2.4)

 

Видно, что период малых колебаний маятника, происходящих под действием силы тяжести, не зависит от массы маятника и амплитуды его колебаний. Однако, если угол отношения велик (a > 6°), колебания перестают быть гармоническими и их период увеличивается с ростом амплитуды. Обозначив

 

,

(2.5)

 

получим аналогичное выражение и для физического маятника:

 

,

(2.6)

 

где L – приведенная длина физического маятника, численно равная длине математического маятника с таким же периодом колебаний. Для определения момента инерции физического маятника относительно оси подвеса О воспользуемся теоремой Штейнера

 

Io = Ic + ml2,

(2.7)

 

где I_c – момент инерции относительно оси, проходящей через центр тяжести; l – расстояние от точки подвеса до центра тяжести.

Формулы (2.4) и (2.6) позволяют, определив из опыта период колебаний маятника, рассчитать ускорение свободного падения

.

Еще в начале XVIII века Галилей установил, что свободное падение – движение тела под действием только силы тяжести, является равноускоренным движением, причем все тела движутся с одинаковым ускорением – g (от лат. gravitas – тяжесть).

Этот экспериментальный факт является следствием установленного Ньютоном закона всемирного тяготения. Сила тяготения, действующая на любое тело со стороны Земли (M_з) вблизи ее поверхности, пропорциональна его массе m:

 

,

 

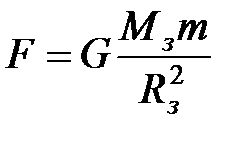где G – гравитационная постоянная; R_з – радиус Земли. Поэтому ускорение, сообщаемое телу силой тяготения, не зависит от массы тела:

 

.

Ускорение свободного падения зависит от широты местности. Это обусловлено особенностями формы земного шара, а также тем, что сила тяготения вызывает не только падение тел на Землю, но и их вращение вокруг земной оси. Ускорение свободного падения на полюсе имеет максимальное значение, так как там отсутствует вращательное движение: g = 9,83м/с². На экваторе, где линейная скорость точек земной поверхности максимальна, ускорения имеет наименьшее значение: g = 9,78 м/с². В задачах обычно принимается среднее значение g = 9,8 м/с².