Главная | Обратная связь

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ

ЖИДКОСТИ ПО МЕТОДУ СТОКСА

 

Цель работы: изучение основных законов внутреннего трения и определение коэффициента вязкости жидкости методом Стокса.

Приборы и принадлежности: сосуд с исследуемой жидкостью, шарик, секундомер, микрометр, линейка.

 

Теория метода

Вязкость, или внутреннее трение, относится к группе явлений, с помощью которых система переходит в равновесное состояние и называемых явлениями переноса. Условием их возникновения является существование различия какого-либо параметра в разных частях системы. В частности, внутреннее трение возникает при различии в скоростях упорядоченного движения жидкости или газа. Распределение скоростей в жидкости характеризуется градиентом скорости – величиной, показывающей, как быстро меняется скорость при перемещении на единицу длины в направлении, перпендикулярном вектору скорости слоев (рис. 3.1). Модуль этой величины определяется формулой

.

 

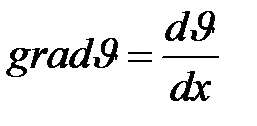Рис. 3.1. Неравномерное распределение скоростей направленного движения жидкости

 

Вязкость (внутреннее трение) характеризует свойства газообразных и жидких тел оказывать сопротивление относительному перемещению слоев вещества. В результате такого перемещения возникает сила, направленная в сторону противоположную скорости движения, – сила внутреннего трения.

Силы, возникающие между слоями газа или жидкости, испытывающими относительное перемещение, называют силами внутреннего трения. Свойства жидкости, связанные с наличием сил внутреннего трения, называют вязкостью.

Между соприкасающимися слоями жидкости при наличии градиента скорости возникают силы, направленные вдоль плоскости соприкосновения и препятствующие их относительному перемещению, – силы внутреннего трения. Их величина определяется законом Ньютона

,

где S – площадь соприкосновения слоев; η – динамический коэффициент вязкости; gradu – градиент скорости.

Динамический коэффициент вязкости численно равен силе внутреннего трения, действующей на единицу площади соприкосновения слоев при градиенте скорости, равном единице. В СИ единица измерения динамического коэффициента вязкости – Паскаль × секунда (Па∙с).

Возникновение вязкости у газов обусловлено переносом импульса упорядоченного движения молекул газа из слоя в слой при хаотическом тепловом движении практически не взаимодействующих молекул, поэтому с ростом температуры вязкость газов возрастает. Иной механизм внутреннего трения в жидкости. Он определяется главным образом силами молекулярного взаимодействия. Так как расстояния между молекулами жидкости существенно меньше, чем в газе, то молекулы испытывают значительные силы притяжения, которые и обусловливают большую вязкость жидкости. Кроме сил притяжения, между молекулами существуют и силы отталкивания, препятствующие сближению молекул. Совместное действие этих сил приводит к тому, что для каждой молекулы существует положение равновесия, около которого оно колеблется в течение некоторого времени (10^-10 с), называемого временем оседлости. По истечении этого времени молекула перемещается в новое положение равновесия на расстоянии 10^-10 м. При повышении температуры Т энергия колебательного движения молекул возрастает, уменьшается время оседлости и коэффициент вязкости экспоненциально падает.

Вязкость жидкости имеет большое практическое значение. Например, без знания вязкости нельзя рассчитать энергию, необходимую для перекачивания жидкости по трубам (нефти в нефтепроводах, воды в водопроводах), рассчитать смазку машин. Вязкость расплавленного шлака играет важную роль в мартеновском и доменном производствах.

Существуют разные методы определения коэффициента вязкости. В данной работе используется один из наиболее простых – метод Стокса. Он основан на измерении скорости шарика, падающего в исследуемой жидкости. Сила внутреннего трения действует и на тело, движущееся в реальной неподвижной жидкости, так как вследствие явления смачивания окружающая тело жидкость движется со скоростью, равной скорости тела.

Движение тела под действием силы тяжести в вязкой среде сопровождается трением и не является свободным падением. Сила вязкого трения пропорциональна скорости тела, поэтому в результате совместного действия неизменных (сила тяжести сила Архимеда ) и переменной (сила трения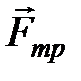 )сил устанавливается равномерное движение, соответствующее равенству нулю результирующей силы, действующей на тело.

Рассмотрим падение тела в вязкой жидкости из состояния покоя. По второму закону Ньютона

 

.

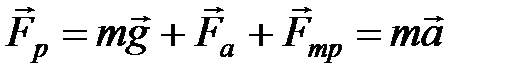(3.1)

 

Ускорение 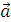, приобретаемое телом, не остается постоянным, так как увеличение скорости приводит к увеличению силы трения, а следовательно, уменьшению равнодействующей 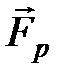. При достаточной продолжительности падения ускорение уменьшается до нуля и дальнейшее движение становится равномерным. В проекции на направление движения уравнение (3.1) примет вид

 

.

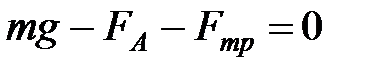(3.2)

 

Достигнутая скорость зависит от формы тела. Так, установлено, что из-за трения в воздухе движение с раскрытым парашютом осуществляется со скоростью ≈ 5 м/с, а без него – 60 м/с. Установившаяся скорость дождевых капель (r = 1–2мм) независимо от высоты облачности ≈ 8 м/с.

Для практических расчетов силы вязкого трения используются эмпирические формулы, учитывающие особенности движения и форму тела, движущегося в жидкости. В середине XIX века английский физик Д. Стокс установил для тел сферической формы малых размеров (радиусом r) зависимость силы вязкого трения и скорости движения

.

(3.3)

Используемый для определения вязкости в методе Стокса шарик изготовлен из материала, хорошо смачиваемого жидкостью, поэтому к его поверхности «прилипает» концентрический слой жидкости, неподвижный относительно шарика. Между этим слоем, движущимся со скоростью шарика, и остальной (неподвижной) жидкостью возникает сила внутреннего трения F_тр, направленная против скорости шарика, т.е. вверх (рис. 3.2).

 

Рис. 3.2. Силы, действующие на шарик при падении в жидкости

 

Получим формулу для скорости установившегося движения шарика в вязкой жидкости. Для шарика радиусом r и плотностью вещества ρ₁, падающего в жидкости с плотностью ρ₂, определим действующие на него силы: сила тяжести 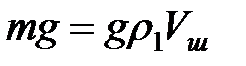, где V_ш – объем шарика; cила Архимеда cила вязкого трения .

Для установившегося движения (u = const, a = 0)

,

,

.

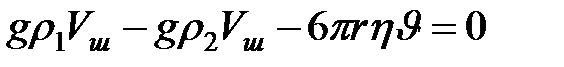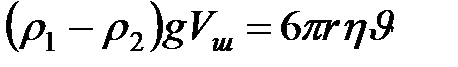Отсюда, учитывая, что объем шара , получим

.

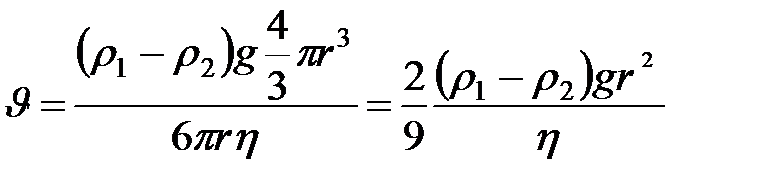(3.4)

Скорость установившегося движения тела легко определить экспериментально как отношение пройденного им пути S ко времени t:

,

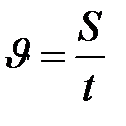Это позволяет использовать формулу (3.4) для определения коэффициента вязкости

.

(3.5)

где d – диаметр шарика; ρ₁ – плотность материала шарика; ρ₂ – плотность исследуемой жидкости; – скорость установившегося движения шарика в жидкости; g – ускорение свободного падения.