Главная | Обратная связь

Общий подход к вероятностной оценке устойчивости ОЭ

 

Вероятностная оценка устойчивости ОЭ предполагает определение вероятности ее нарушения (или сохранения) в условиях ЧС. Общий подход к оценке изложен в работе [19].

Нарушение (потеря) устойчивости ОЭ зависит от возможности проявления опасных явлений в районе его расположения; интенсивности, порождаемых опасными явлениями поражающих факторов, действующих на объект; устойчивости объекта. Поэтому вероятность нарушения устойчивости ОЭ представляет собой произведение вероятности исходного события на условную вероятность получения объектом недопустимых (неприемлемых) повреждений при условии, что исходное событие было. Исходным событием в данном случае является критическая (ее можно также назвать пороговой) ситуация, при которой реализуются поражающие факторы опасного явления с параметрами, превышающими порог (предел) устойчивости ОЭ. Вероятность исходного события, таким образом, представляет собой произведение вероятности опасного явления на условную вероятность превышения поражающими факторами предела устойчивости ОЭ.

Недопустимыми повреждениями ОЭ или его элементов являются повреждения, при получении которых объект не может выполнять заданные функции.

Опасные явления, которыми могут быть природные явления (землетрясения, наводнения и т.п.), техногенные аварии и катастрофы, явления, связанные с применением оружия в военное время, являются редкими событиями. Поэтому их распределение во времени может быть представлено простейшим пуассоновским потоком случайных событий, обладающих свойствами стационарности, ординарности и отсутствия последействия. Для такого потока случайное число событий, происходящих за интервал времени , определяется законом Пуассона

, (3.83)

где - вероятность событий за интервал времени , - математическое ожидание числа проявлений опасного явления за время (параметр распределения Пуассона), 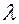- интенсивность событий.

В общем случае опасные явления не всегда подчиняются закону Пуассона. Например, для землетрясений характерна цикличность, т.е. нарушение свойств последействия. Тем не менее при оценках воздействий на ОЭ со сроком эксплуатации, соизмеримым с периодичностью явлений, их поток в первом приближении может считаться пуассоновским.

Для пуассоновского потока время между событиями подчиняется экспоненциальному закону и вероятность хотя бы одного проявления опасного явления за интервал времени с учетом (3.83) определяется зависимостью:

, (3.84)

где - вероятность невозникновения опасного явления в течение времени .

Для редких событий при вероятность хотя бы одного проявления опасного явления за время может быть приближенно записана в виде:

.

Уровни поражающих факторов опасного явления, определяющие их поражающее действие, будем характеризовать параметрами q_H . Из-за неопределенности взаимного положения источника опасности и ОЭ, а также других факторов, нагрузку от поражающих факторов, действующую на ОЭ, следует рассматривать как случайную величину Q_H, полной вероятностной характеристикой которой является функция распределения F_H(q)=P(Q_H<q_H).

Критическую нагрузку, при которой устойчивость ОЭ еще не нарушается, обозначим через q_K. Она характеризует устойчивость ОЭ по отношению к рассматриваемому поражающему фактору. Из-за случайного разброса характеристик объектов, неопределенности их состояния в момент действия поражающего фактора и других не учитываемых обстоятельств критическую нагрузку также следует рассматривать как случайную величину Q_K. Вероятностной характеристикой критической нагрузки будет являться функция распределения F_к(q)=P(Q_к<q_к), которую обычно называют физическим или условным законом поражения.

Очевидно, что устойчивость ОЭ может быть нарушена, если уровень поражающего фактора превышает критическую нагрузку, т.е. условие возможного нарушения устойчивости ОЭ должно быть записано в виде:

Q_H>Q_K . (3.85)

Вероятность выполнения условия (3.58) является условной вероятностью возникновения критической ситуации, связанной с возможной потерей устойчивости ОЭ P_KC=P(Q_H>Q_K) при условии, что опасное явление в районе ОЭ имело место. Если D[Q_H]>> D[Q_K] , то разбросом критической нагрузки можно пренебречь, и считать ее детерминированной величиной Q_K q_K . Тогда P_KC=P(Q_H>q_K) .

Величина P_KC в общем случае вычисляется по заданным законам распределения действующей нагрузки и устойчивости ОЭ.

Зависимость вероятности поражения объектов с устойчивостью q_K от расстояния до возможного источника опасного явления P_KC(r)=P(Q_H(r)>q_K) называют координатным законом поражения. По заданному уровню веро-ятности P_KC его можно аппроксимировать ступенчатым законом. Все объекты с устойчивостью q_K внутри этой зоны будут получать недопустимые повреждения, т.е. терять устойчивость, с вероятностью не ниже P_KC . Если эта зона круг, то она будет характеризоваться радиусом зоны потери устойчивости R_ПУ. Угроза потери устойчивости для объекта наступает с его попаданием в эту зону.

Если возможно разновременное возникновение нескольких видов опасных явлений, то математическое ожидание числа критических ситуаций может быть определено по формуле ,где m - число видов опасных явлений в районе ОЭ, .

Вероятность возникновения хотя бы одной критической ситуации в этом случае вычисляется по формуле

. (3.86)

По разным причинам устойчивость ОЭ и действующие на них нагрузки с течением времени изменяются. Поэтому в общем случае случайные величины Q_K и Q_H должны быть представлены в виде некоторых зависимостей Q_K(t) и Q_H(t) , а выражение (3.86) записано в виде

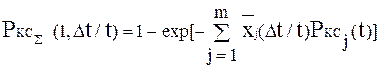, (3.87)

где 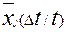- математическое ожидание числа опасных явлений j-го вида в районе ОЭ в рассматриваемое время, .

Для определения вероятности (1,Dt) при наличии соответствующих исходных данных могут быть использованы статистический, либо вероятностный методы. Статистический метод может быть применен для типовых ОЭ, размещенных и эксплуатируемых в примерно одинаковых условиях и при наличии достаточно представительной статистики. В этом случае

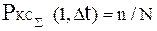, (3.88)

где n и N соответственно число критических ситуаций и ОЭ, нахо-дящихся в эксплуатации в течение рассматриваемого интервала времени.

Для редких событий вероятность рассчитывается по формуле (3.86). При этом параметр Пуассона (математическое ожидание числа критических ситуаций) может быть определен с использованием зависимостей:

(3.89)

и . (3.90)

В формуле (3.89) - интенсивность критических ситуаций, К - число критических ситуаций на ОЭ рассматриваемого типа за время , в течение которого интенсивность остается неизменной; - суммарная наработка всех ОЭ в течение времени , объекто-лет; t_i – время эксплуатации i-го ОЭ.

В формуле (3.90) S_ОЯj – площадь района, в пределах которого проявляется j-е опасное явление; SKH_j - площадь зоны района проявления j-го опасно-го явления, где действуют поражающие факторы, превышающие предел устойчивости ОЭ. Применение формулы (3.90) оправдано в предположении, что местонахождение ОЭ, очагов или эпицентров опасного явления распределено внутри области S_OЯ равномерно, а зона S_KH<<S_OЯ и они не пересекаются.

Достижение и даже превышение поражающим факторами предела устойчивости ОЭ еще не означает потери объектом устойчивости. Это происходит с определенной вероятностью, которая может быть определена с использованием структурно-логических схем (деревьев событий), в данном случае деревьев устойчивости и неустойчивости, показанных на рисунках 3.12 и 3.13.

Из структуры деревьев следует, что устойчивость ОЭ обеспечивается, если устойчив каждый из его структурных элементов и наоборот. В смысле устойчивости это означает, что ОЭ с нерезервированными элементами следует рассматривать как последовательное соединение элементов, а вероятность потери устойчивости (получения неприемлемых повреждений).

P_HПОЭ и ее сохранения R_НПОЭ определять, используя зависимости:

и , (3.91)

где - вероятность неполучения неприемлемых повреждений i-ым структурным элементом ОЭ. Вероятности получения или неполучения неприемлемых повреждений и структурными элементами ОЭ при определенных нагрузках устанавливается с использованием методов математического моделирования, данных модельных, натурных экспериментов и реальных ЧС.

Решающую роль в потере или сохранении устойчивости, как следует из формул (3.91) играет наиболее слабый элемент.

С учетом вероятности получения неприемлемых повреждений при нагрузках, соответствующих критической ситуации, вероятность потери устойчивости ОЭ при i-ой нагрузке в j-ой критической ситуации должна быть записана в виде:

, (3.92)

где РНП_ОЭji - вероятность получения неприемлемых повреждений ОЭ при i-ой нагрузке в j-ой критической ситуации.

Характеристика устойчивости совпадает с характеристикой уязвимости (получением неприемлемых повреждений), определяемой как критическая нагрузка , начиная с которой наступает критическая ситуация с возможной потерей устойчивости ОЭ.

Таким образом, приемлемые и неприемлемые повреждения при нагрузках, равных пределу устойчивости, равновероятны, и их вероятности равны 0,5. При бόльших значениях нагрузок вероятность неприемлемых повреждений возрастает, достигая в пределе 1. Вероятность потери устойчивости ОЭ с учетом всех возможных критических ситуаций и нагрузок, равных пределу устойчивости, может быть представлена в виде:

(3.93)

Пример.

Определить вероятность потери устойчивости ОЭ при достижении поражающими факторами опасных явлений его пределов устойчивости. ОЭ расположен в сейсмоопасном районе с частостью землетрясений 0,1 год^-1 . В соответствии с прогнозом очаг землетрясения может быть расположен на глубине h=10 км. Интенсивность землетрясения в очаге I₀=9 баллов. В районе ОЭ также может возникнуть очаг поражения в результате взрыва газовоздушной смеси при аварии на магистральном газопроводе. Масса пропана в окружающей среде может достигать М₀=500 т. Частость взрывов 0,08 год^-1. Время эксплуатации ОЭ Δt=25 лет. Пределы устойчивости объекта к землетрясениям – 7 баллов, к ударной волне взрыва – 30 кПа.

Решение.

1. Пользуясь зависимостями для интенсивности землетрясения I и избыточного давления на фронте воздушной ударной волны при наземном взрыве газовоздушной смеси ΔР_ф , определяем радиусы площадей районов проявления опасных явлений и их зон, в пределах которых действуют нагрузки, превышающие пределы устойчивости ОЭ. Границами районов проявления опасных явлений считаем окружности с интенсивностью землетрясений I=3 балла, при которой начинаются поражения, и избыточном давлении ударной волн ΔР_ф=10 кПа, соответствующем границе очага поражения.

Радиусы площадей района проявления землетрясения и зоны нагрузок, превышающих предел устойчивости ОЭ:

 

 

Радиусы площадей района очага поражения при взрыве ГВС и зоны нагрузок, превышающих предел устойчивости ОЭ:

 

 

где - радиус газовоздушного облака, ω – коэффициент участия газа в образовании облака.

2. Определяем математическое ожидание числа критических ситуаций (параметр Пуассона) за время эксплуатации объекта

3. 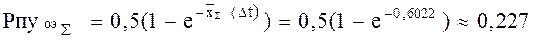3. Определяем вероятность нарушения устойчивости ОЭ