 |
|
Практические занятия 2.
Определители 3-го порядка.
Вычисление и свойства определителей 3-го порядка
Пусть дана квадратная матрица третьего порядка:
Определителем третьего порядка называется число, обозначаемое символом
и вычисляемое по правилу Саррюса:
.
Произведения этих элементов Произведения этих элементов
берем со своими знаками берем с противоположными
знаками
Пример 1. Вычислить определитель матрицы 
.
Решить задачи:
В задачах требуется вычислить определители третьего порядка.
1.24. 
.
1.25. 
.
1.26. 
.
1.27.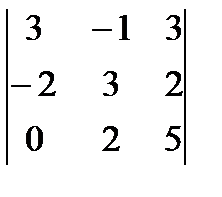 
.
1.28.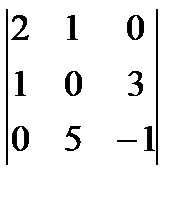 
.
1.29. 
.
1.30. 
.
1.31. Определитель матрицы 
равен
1.32.Определитель матрицы равен
1.33.Определитель матрицы 
равен
1.34. Вычислить определитель 
.
1.35. Вычислить определитель 
1.36. Вычислить определитель 
.
1.37. Вычислить определитель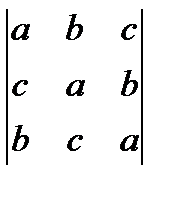 
.
1.38.Доказать справедливость равенств:
1) 
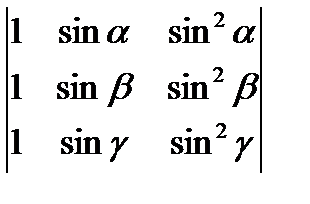= (sin α —sin β) (sin β—sin γ)(sin γ — sin α);
2) 
= 
1.39. Решить уравнения:
1) 
= 0 2) 
= 0
1.40. Решить неравенства:
1) 
< 1 2) 
> 0
Практические занятия 3
Определители 4-го и более высоких порядков.
Вычисление и свойства определителей 4-го и более высоких порядков
Минором некоторого элемента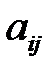 
определителя n–го порядка называется определитель (n-1)–го порядка, полученный из исходного путем мысленного вычеркивания строки и столбца на пересечении которых находится выбранный элемент. Обозначается 
.
Например, если 
, то 
, 
.
Алгебраическим дополнением элемента 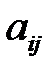определителя называется его минор, взятый со знаком «плюс», если сумма 
– четное число, и со знаком «минус», если эта сумма нечетная. Обозначается 
.
Пример 1. Вычислить определитель матрицы 
.
Решение: Для разложения определителя обычно выбирают тот ряд, где есть нулевые элементы, т. к. соответствующие им слагаемые в разложение будут равны нулю.
.
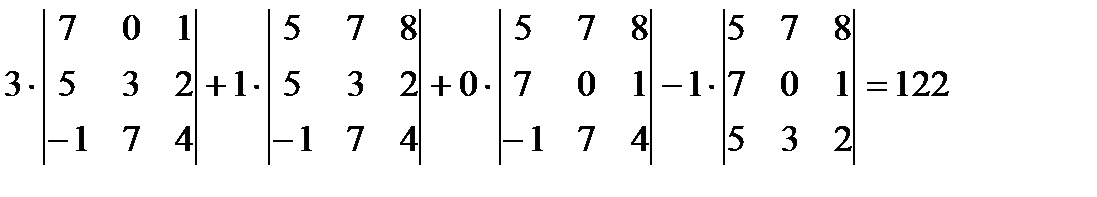Решить задачи:
1.41. Определитель 
равен…
1.42. Определитель 
равен…
1.43. Определитель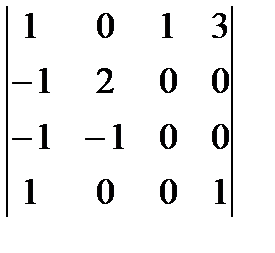 
равен…
В задачах 1.44.- 1.52 требуется вычислить определители четвёртого порядка.
1.44. 
. 1.45.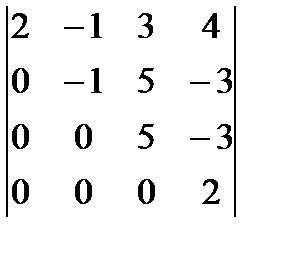 
1.46. 
. 1.47. 
.
1.48.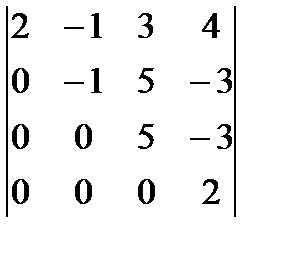 
. 1.49. 
.
1.50. 
. 1.51. 
.
1.52.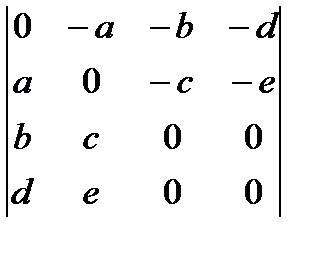 
Практическое занятие 4
Решение систем линейных уравнений методом Крамера