 |
|
Примеры заданий с решениями по теме
Задание №1. Индукция магнитного поля в вакууме вблизи плоской поверхности магнетика равна 
, а вектор 
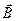составляет угол 
с нормалью к границе раздела. Магнитная проницаемость магнетика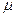 
. Найти: 1) поток вектора 
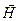через поверхность сферы радиуса 
с центром, совпадающим с вектором 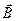и лежащим на поверхности магнетика; 2) циркуляцию вектора 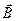по квадратному контуру Г со стороной 
. Точка пересечения диагоналей контура лежит на поверхности, а две противоположные стороны параллельны ей.
Решение:
Поток вектора 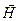через замкнутую поверхность определяется соотношением (теоремой Гаусса в интегральной форме):
(1)
Сферу пронизывает как вектор 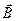, находящийся в вакууме, так и вектор 
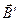- в среде, причем поток зависит от угла между нормалью 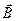и и 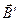в вакууме и среде соответственно.
Следовательно, вклад в поток вносят только нормальные компоненты векторов напряженности магнитного поля и магнитной индукции. Условия для них имеют вид:
рис. 6
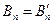(2)
(3)
Так как по условию задачи угол между нормалью и 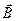в вакууме равен , а вектора магнитных и электрических полей, проходя через границу раздела сред, преломляются под разными углами, то между нормалью и 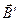будет угол 
, который определяется с помощью соотношения (2)
(4)
Вектор 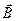выходит из рассматриваемой сферы по условию задачи, следовательно, его поток положительный, а вектор 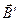входит, следовательно, его поток отрицательный. Результирующий поток равен сумме соответствующих потоков с учетом их знаков.
(5)
где 
- площадь соответствующей замкнутой поверхности (поверхности полусферы в вакууме и соответственно такой же полусферы в среде).
Связь между компонентами векторов магнитной индукции и напряженностью магнитного поля имеет вид:
(6)
(7)
Подставляя (4), (6) и (7) в (5), получаем искомый поток:
(8)
Циркуляция вектора магнитной индукции в общем случае определяется как (теорема Стокса в интегральной форме):
(9)
В силу симметрии задачи на участках перпендикулярных к границе раздела циркуляция взаимно компенсируется и равна нулю. Следовательно, вклад дают только тангенциальные компоненты векторов магнитной индукции:
(10)
Учитывая, что поле в пределах одной среды однородно и , получаем:
(11)
Тангенциальная компонента вектора 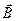по условию определяется соотношением:
(12)
Подставляя (12) в (11) получаем соотношение для искомой циркуляции:
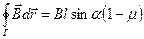(13)
Ответ: 
; .
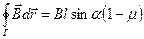Задание №2. Круговой контур с током лежит на плоской границе вакуума и магнетика. Проницаемость последнего равна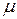 
. Найти индукцию 
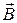магнитного поля в произвольной точке на оси контура, если индукция поля в этой точке в отсутствие магнетика равна 
. Обобщить полученный результат на все поле.
Решение:
Так как по условию задачи причиной возникновения магнитного поля является ток, текущий по круговому контуру, находящемуся на границе раздела вакуум – магнетик, то можно считать, что вектора магнитной индукции и напряженности магнитного поля имеют только нормальную компоненту в любой точке на оси, проходящей через центр кругового тока и перпендикулярной к нему. Тангенциальные компоненты в данном случае оказываются взаимно скомпенсированными. Для соответствующих напряженностей при этом выполняется закон полного тока (Эрстеда):
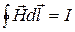(1)
рис.7
Учитывая, что магнитное поле возникает на границе раздела сред интеграл (1) распадается на сумму двух интегралов, соответственно в вакууме и магнетике:
(2)
где 
- элемент силовой линии, проходящей через центр кругового тока, вдоль которой циркулирует вектор напряженности магнитного поля.
Выразим напряженности через соответствующее значение вектора магнитной индукции 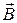, как в вакууме, так и в магнетике:
(3)
(4)
Подставляя (3) и (4) в (2) и считая, что магнетик изотропная среда получаем:
(5)
Объединив интегралы в левой части (5), получаем:
(6)
С другой стороны в отсутствии магнетика закон полного тока примет вид:
(7)
Сравнивая левые части (7) в (6) и учитывая, что интегрирование ведется по одной и той же переменной, получаем:
(8)
При учете сонаправленности векторов магнитной индукции вдоль оси кругового тока (как было сказано ранее это только нормальные компоненты) соотношение (8) может быть переписано в векторной форме:
(9)
Ответ: .