Главная | Обратная связь

Природне і поляризоване світло. Закон Малюса

Наслідком теорії Максвелла є твердження про поперечність світлових хвиль: вектори напруженості електричного і магнітного полів електромагнітної хвилі взаємно перпендикулярні і коливаються перпендикулярно до вектора швидкості поширення хвилі. При розгляді світлових електромагнітних хвиль усі міркування зазвичай проводять для вектора , який називається світловим вектором, тому що він має визначальний вплив при дії світла на речовину. Площина, в якій відбувається коливання вектора , називається площиною поляризації, а перпендикулярна до неї площина – площиною коливань.

Світло є сумарним електромагнітним випромінюванням множини атомів. Атоми випромінюють світлові хвилі незалежно один від одного у вигляді хвильового цугу, в якому вектор коливається в одній площині. Хвильові цуги неперервно накладаючись змінюють один одного. Тому світлова хвиля, що випромінюється тілом, характеризується рівноймовірними напрямками коливань світлового вектора .

Природним (неполяризованим) називається світло з усіма можливими рівноймовірними орієнтаціями вектора (отже, і ) (рис. 2.14,а).

Поляризованим називається світло, в якому напрямки коливань вектора певним чином упорядковані.

Якщо коливання вектора світлової хвилі відбуваються в одній певній площині, то світло називається лінійно поляризованим (плоскополяризованим (рис. 2.14,б). У випадку, коливектор описує еліпс в площині перпендикулярній до напрямку поширення променя, то така хвиля називається еліптично поляризованою, а якщо коло - поляризованою по колу (циркулярно поляризованою).

Коли вектор обертається проти годинникової стрілки в площині перпендикулярній до напрямку поширення променя, то поляризація називається правою, а в протилежному випадку – лівою.

Поляризацією світла називається виділення лінійно поляризованого світла з природного або частково поляризованого.

Плоскополяризоване світло можна отримати з природного за допомогою приладів, які називаються поляризаторами. Ці прилади вільно пропускають коливання, паралельні до площини поляризації, яка називається головною площиною, і повністю або частково затримують коливання, які перпендикулярні цій площині. В ролі поляризаторів можуть бути середовища, які анізотропні відносно коливань вектора , наприклад, кристали. Одним із природних кристалів, які використовуються як поляризатори, є турмалін. Прилади, за допомогою яких аналізують ступінь поляризації світла, називають аналізаторами.

Якщо на поляризатор падає природне світло (рис. 2.15), то при вході в поляризатор падаючу хвилю, вектор напруженості електричного поля якої коливається у площині, що утворює з головною площиною поляризатора р–р кут 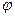, можна зобразити у вигляді двох коливань у взаємно перпендикулярних площинах (рис. 2.15). Причому амплітуди коливань можна виразити таким чином:

; .

Перше коливання з амплітудою пройде через поляризатор, а друге з амплітудою буде затримане поляризатором. Отже, при цьому . Оскільки інтенсивність світла пропорційна квадратові амплітуди світлового вектора ( ), то співвідношення можна записати таким чином:

, (2.38)

де – інтенсивність коливань з амплітудою .

В природному світлі всі значення j рівноймовірні. Тому частка світла, що пройшло через поляризатор, буде дорівнювати середньому значенню , тобто і

.

Якщо на аналізатор падає лінійно поляризоване світло, отримане за допомогою поляризатора, головна площина якого p–p утворює кут 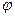з головною площиною аналізатора a–a, то значення інтенсивності світла на виході з аналізатора буде виражатися формулою

. (2.39)

Якщо аналізатор і поляризатор не є абсолютно прозорими, то

, (2.40)

де – кофіцієнт прозорості поляризатора, - коефіцієнт прозорості аналізатора.

Отримані співвідношення (2.39) і (2.40) виражають закон Малюса.