 |
|
Обертання площини поляризації світла
Явище обертання площини поляризації світлової хвилі на деякий кут при проходженні світла крізь кристалічні тіла і деякі ізотропні рідини, називається обертанням площини поляризації або оптичною активністю.
Якщо речовина не знаходиться у зовнішньому магнітному полі, то оптична активність буде природною.
Нехай погляд спостерігача спрямований назустріч падаючому променю. Обертання називають правим (додатним), якщо площина поляризації повертається вправо (за годинниковою стрілкою) для спостерігача, і лівим (від’ємним), якщо вона повертається вліво. Кут обертання площини поляризації пропорційний до товщини шару оптично активної речовини:
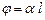, (2.42)
де 
– довжина шляху променя в оптично активному середовищі; 
– коефіцієнт пропорційності, який називають обертальною здатністю, або питомим обертанням, залежить від природи речовини, від температури та довжини хвилі світла.
Питоме обертання дорівнює величині кута, на який повертається площина поляризації монохроматичного світла при проходженні шару завтовшки 1 м.
Для оптично активних рідин та розчинів Ж.Біо встановив, що кут повороту площини поляризації прямо пропорційний товщині шару l і концентрації C оптично активної речовини, тобто
, (2.43)
Коефіцієнт пропорційності 
називається питомим обертанням розчину залежить від природи оптично активної речовини, розчинника, їх температури та довжини світлової хвилі.
Властивості оптичної активності розчинів дають змогу визначити їх концентрації. Прилади, за допомогою яких проводять такі вимірювання, називаються поляриметрами. Оскільки для розчину цукру питоме обертання значне, то поляриметри набули широкого застосування в цукрометрії.
Теорію обертання площини поляризації оптично активними речовинами розробив О. Френель. Він вважав, що це явище зумовлене особливим видом подвійного заломлення променів, при якому швидкість поширення світла в активному середовищі різна для променів, що мають праву і ліву колові поляризації.
У 1845 р. М. Фарадей встановив, що при поширенні лінійно поляризованого світла в оптично неактивних речовинах в напрямку магнітного поля відбувається поворот площини поляризації на деякий кут. Досліди М. Фарадея та М. Верде показали, що кут повертання площини поляризації пропорційний довжині шляху l променя у речовині і напруженості 
магнітного поля, тобто
, (2.44)
де V – стала Верде, яка залежить від природи речовини і довжини хвилі світла.
Сталу Верде для оптично неактивних рідин можна визначити, якщо розмістити трубку з рідиною в соленоїді і пропустити через його обмотку струм. Тоді напруженість магнітного поля всередині соленоїда (рідині) визначається з формули
, (2.45)
де 
– сила струму, що протікає через соленоїд, 
– кількість витків соленоїда,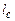 
– довжина соленоїда.
З врахуванням останньої формули отримаємо, що при умові 
. (2.46)
Згідно (2.46) графік залежності 
має вигляд прямої лінії, з нахилу якої 
можна вирахувати сталу Верде
. (2.47)
§2.4. Дисперсія світла
Дисперсією світла називається залежність показника заломлення n середовища від частоти 
(довжини хвилі 
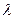) світла або залежність фазової швидкості 
світла в середовищі від його частоти .
Дисперсію світла представляють у вигляді залежності 
. Наслідком дисперсії є розклад у спектр пучка білого світла.
Розглянемо дисперсію світла у призмі. Нехай монохроматичний пучок світла падає на призму з показником заломлення n під кутом 
(рис. 2.17). Кут 
– заломлюючий кут призми. Із рис. 2.17 видно, що кут відхилення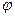 
дорівнює:
.
Нехай кути і 
малі, тоді кути 
, 
і 
також будуть малі і синуси цих кутів дорівнюватимуть кутам. Тому
, 
.
Оскільки 
, то
,
і 
.
В результаті
, (2.48)
тобто кут відхилення променів призмою тим більший, чим більший заломлюючий кут призми. Оскільки кут відхилення 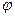залежить від величини 
, а n є функцією довжини хвилі, то промені різних довжин хвиль після проходження призми виявляються відхиленими на різні кути.
Кутовою дисперсією призми, що відповідає сталому значенню кута падіння , називається величина
. (2.49)
Кут відхилення 
буде мінімальним, коли промінь проходить через призму паралельно до її основи. За такої умови 
і 
, тоді
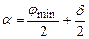, а 
.
Згідно із законом заломлення
. (2.50)
Звідси
.
Тоді
. (2.51)
Для спектральних приладів призми виготовляють здебільшого із заломлюючими кутами 
. Тоді
, де 
. (2.52)
За допомогою призми, як і за допомогою дифракційної гратки можна визначити спектральний склад світла.
Величина, яка показує, як швидко змінюється показник заломлення п речовини з довжиною хвилі 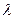називається дисперсією речовини D:
. (2.53)
Дисперсію світла в середовищі називають нормальною, якщо із зростанням частоти світла абсолютний показник заломлення n середовища також зростає:
, 
.
Така залежність показника заломлення n від буде в тих областях частот, для яких середовище прозоре. Наприклад, звичайне скло прозоре для видимого світла і в цьому інтервалі частот має нормальну дисперсію.
Дисперсію світла в середовищі називають аномальною, якщо із зростанням частоти світла абсолютний показник заломлення середовища n зменшується:
, 
.
Аномальна дисперсія буде в області частот, які відповідають смугам інтенсивного поглинання світла речовиною
В різних ділянках спектра дисперсія характеризується тією зміною показника заломлення, яка припадає на одиничний інтервал довжин хвиль. Ця величина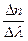 
називається середньою дисперсією для ділянки спектра , 
.
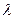У довідникових таблицях показники заломлення 
різних речовин даються для жовтої лінії натрію 
=0,5893мкм і позначаються 
. Середня дисперсія визначається за синьою 
=0,4861мкм і червоною 
=0,6563мкм лініях водню і позначається 
. Величина 
називається відносною дисперсією, обернена її величина – коефіцієнтом дисперсії.
Поглинання світла
Поглинанням світла називається явище втрати енергії світловою хвилею, яка проходить через речовину, внаслідок перетворення енергії хвилі у інші форми енергії.
При проходженні паралельного пучка світла крізь шар прозорого середовища його інтенсивність зменшується. Поглинання світла може приводити до нагрівання, іонізації або збудження атомів і молекул речовини, до деформації. Поглинання може супроводжуватись розсіянням світла та індуктивним випромінюванням.
Щоб одержати співвідношення, яке виражає закон поглинання світла, розглянемо шар прозорого середовища завтовшки l, на який падає паралельний пучок променів інтенсивністю 
(рис. 2.18). Виділимо в середовищі нескінченно тонкий шар dl, який обмежений паралельними поверхнями, що перпендикулярні до напрямку поширення світла. Дослід показує, що зменшення інтенсивності світла шаром середовища dl пропорційне до величини інтенсивності, що входить у цей шар, і товщини шару, тобто
,
де 
– коефіцієнт пропорційності, який не залежить від інтенсивності світла і називається коефіцієнтом поглинання.
Знак мінус вказує на те, що із збільшенням товщини шару поглинаючого середовища інтенсивність світла, що проходить крізь нього, зменшується.
Після розділення змінних у рівнянні дістаємо
.
Проінтегруємо це рівняння:
; 
.
В результаті маємо, що
, (2.54)
де І – інтенсивність світла, що виходить із шару поглинаючого середовища завтовшки l.
При 
інтенсивність 
. Отже, шар, товщина якого дорівнює 
, зменшує інтенсивність світла в е разів. Співвідношення (2.54) було встановлене у 1729 р. П. Бугером і називається законом Бугера, або законом Бугера-Ламберта.
А. Бер встановив, що поглинання світла розчинами пропорційне молекулярній концентрації 
розчиненої речовини, тобто
,
де 
– коефіцієнт пропорційності. який залежить від природи розчиненої речовини і не залежить від її концентрації.
Тоді закону Бугера-Ламберта-Бера, який справедливий для газів і розчинів малих концентрацій, можна надати вигляду
. (2.55)
Рекомендована література до Розділу ІІ
1. І.Р. Зачек, І.М. Кравчук, Б.М. Романишин, В.М. Габа, Ф.М. Гончар. Курс фізики: Навчальний підручник/ За ред. І.Е. Лопатинського. – Львів: Бескид-Біт, 2002. 376 с.
2. Б.М. Яворський, А.А. Детлаф. Курс фізики ІІІ, - К.: Вища школа, 1973. 499 с.
3. Т.И. Трофимова. Курс физики. – М.: Высш шк., 1990. 478 с.
4. И.В. Савельев. Курс общей физики, т. ІІІ - М.: Наука, 1986. 318 с.
5. С.Э. Фриш, А.В. Тиморева. Курс общей физики, т. ІІІ. – М.: Физматгиз, 1962. 644 с.