Главная | Обратная связь

Теоретическое введение

При объединении атомов в кристаллическое тело структура энергетических уровней электронов претерпевает важные изменения. Эти изменения почти не затрагивают наиболее глубокие уровни, образующие внутренние, заполненные оболочки. Зато наружные уровни коренным образом перестраиваются. Указанное различие связано с разным пространственным распределением электронов, находящихся на глубоко лежащих и на верхних энергетических уровнях. Атомы в кристалле тесно «прижаты» друг к другу. Волновые функции наружных электронов в существенной мере перекрываются, что приводит к обобществлению этих электронов – они теперь принадлежат не отдельным атомам, а всему кристаллу. В то же время волновые функции внутренних электронов друг с другом практически не перекрываются. Положение этих уровней в кристалле мало отличается от их положения у изолированных атомов.

У одиночных атомов одного и того же элемента энергия соответствующих уровней в точности одинакова. При сближении атомов эти уровни начинают расходиться, как это изображено на рис. 16.1. Расщепление энергетических уровней аналогично расхождению частот колебаний, происходящему при появлении связи между одинаковыми маятниками или между электрическими колебательными контурами, настроенными на одну и ту же частоту. Системы «разошедшихся» уровней образуют в кристалле разрешенные энергетические зоны, разделенные запрещенными зонами (рис. 16.1).

Ширина зон определяется величиной связи между атомами и не зависит от числа атомов в кристалле. В то же время количество уровней в зоне равно числу атомов и описывается цифрами с десятком или даже с несколькими десятками нулей. Таким образом, расстояние между уровнями оказывается столь незначительным, что говорить о положении отдельных уровней в зоне не имеет смысла. В то же время количество уровней сохраняет вполне ясный смысл, так как при сближении атомов число возможных состояний (а, следовательно, и число электронов, которые могут занять эти состояния) не изменяется.

Электропроводность твердых тел определяется распределением электронов по уровням (рис.16.2). В металлах электроны лишь частично заполняют последнюю из занимаемых зон (зона проводимости – ЗП), и в ней имеются свободные состояния. В присутствии электрического поля электроны проводимости могут занимать эти состояния, и металл проводит электрический ток.

В изоляторах (диэлектриках) электроны доверху заполняют последнюю из занятых зон (валентную зону – ВЗ). Следующая разрешенная зона (зона проводимости) не содержит электронов. В присутствии поля ни один из электронов не может изменить своего состояния, так как нет свободных энергетических состояний. Твердое тело будет не проводящим при температуре, равной Т=0 К. Однако при отличной от нуля температуре существует конечная вероятность того, что некоторые электроны будут за счет теплового возбуждения переброшены через энергетическую щель (Е_g – ширина запрещенной зоны – ЗЗ) из валентной зоны в зону проводимости. При этом остаются незанятые уровни в валентной зоне. Термически возбужденные электроны способны переносить ток (переходить на свободные энергетические состояния в зоне проводимости). В валентной зоне проводимость становится возможной из-за появления свободных состояний – дырок, которые ведут себя как свободные носители положительного заряда: ближайший к дырке электрон валентной зоны, попадая в неё, оставляет при этом новую дырку, которую заполнит другой электрон валентной зоны и т.д. Дырка валентной зоны будет перемещаться по кристаллу в направлении, противоположном направлению движения электронов валентной зоны. Таким образом, валентная зона будет зоной дырочной проводимости.

Приведут ли тепловые перебросы электронов из валентной зоны в зону проводимости к заметной проводимости или нет, существенно зависит от ширины запрещенной зоны Е_g, поскольку число электронов, переброшенных в зону проводимости при температуре Т, пропорционально величине (k=1.38∙10^-23 Дж/К – постоянная Больцмана). При Е_g=4 эВ (1эВ=1.6∙10^-19 Дж) эта величина при комнатной температуре (kT≈0.025 эВ) составляет , то есть по сути дела переброса электронов в валентную зону не происходит. Если же Е_g=0.25 эВ, то число переброшенных электронов при комнатной температуре определяется величиной , так что будет наблюдаться заметная проводимость.

Твердые тела, которые являются диэлектриками при Т=0 К, но имеют такую ширину запрещенной зоны Е_g, что тепловое возбуждение при температурах ниже точки плавления может обуславливать заметную проводимость, называются полупроводниками. Ясно, что не существует четкого различия между полупроводниками и диэлектриками; грубо говоря, в наиболее важных полупроводниках Е_g обычно меньше 2 эВ, а часто составляет лишь несколько десятых электрон-вольта. Типичные удельные сопротивления полупроводников при комнатной температуре лежат в интервале между 10^-5 и 10⁷ Ом∙м (в отличие от металлов, где ρ=10^-8 Ом∙м, а также и от хороших диэлектриков, у которых ρ может достигать до 10²⁰ Ом∙м).

Самой важной характеристикой любого полупроводника при температуре Т является число n_c электронов в зоне проводимости, приходящееся на единицу объема, и число дырок p_v на единицу объема в валентной зоне. Эти величины определяются произведением числа уровней, имеющихся в единице объема полупроводника, на вероятность их заполнения. Вероятность заполнения энергетических уровней выражается функцией распределения Ферми f(E). Для анализа электронных состояний необходимо использовать квантовую статистику

, (16.1)

где Е – энергии уровней; μ – химический потенциал. Часто химический потенциал полупроводников называется «уровнем Ферми» (μ=E_F) . Однако, это неудачная терминология. Обычное определение уровня Ферми – энергия, ниже которой при Т=0 К в металле электронные уровни в зоне проводимости заполнены, а выше – свободны (не заполнены). В полупроводниках химический потенциал μ лежит примерно в середине запрещенной зоны, поэтому ни один электронный уровень не совпадает с химическим потенциалом.

Обозначим через Е_с энергию дна зоны проводимости, а через Е_v – энергию потолка валентной зоны (рис. 16.3). В полупроводниках даже при весьма малой ширине запрещенной зоны Е_g=Е_с–Е_v обычно выполняется условие

. (16.2)

Тогда благодаря тому, что каждый уровень электрона в зоне проводимости лежит выше Е_с, а каждый уровень валентной зоны – ниже Е_v, упрощается выражение для функции распределения f(Е) – оно становится классическим (статистика Больцмана).

; Е>Е_с . (16.3)

Так что число электронов n_c в зоне проводимости, приходящееся на единицу объема, будет равно

, (16.4)

где А(Т) – число уровней, имеющихся в зоне проводимости в единице объема полупроводника.

Вероятность появления дырки в валентной зоне определяется разностью:

,

поскольку и . Поэтому число дырок p_v в валентной зоне, приходящееся на единицу объема, будет равно

. (16.5)

Заметим, что А(Т) и В(Т) – медленно меняющиеся функции температуры по сравнению с экспонентами в (16.4) и (16.5).

Если полупроводник является настолько чистым, что примеси вносят пренебрежимо малый вклад в концентрацию носителей, то мы имеем дело с собственным полупроводником. В нем электроны могут попасть в зону проводимости, только покинув заполненные ранее уровни в валентной зоне, оставив вместо себя там дырки. Таким образом, число электронов в зоне проводимости равно числу дырок в валентной зоне n_c(T)=p_v(T)=n. Так что из (16.4) и (16.5) можно записать

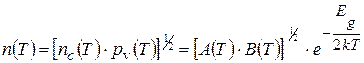. (16.6)

Найдем теперь электропроводность полупроводника. В присутствии поля большая часть электронов в зоне проводимости начинает двигаться в сторону, противоположную полю. Средняя величина скорости электронов перестает быть равной нулю и направлена вдоль поля. При этом вплоть до самых сильных полей (практически до пробоя) выполняется формула

, (16.7)

где – среднее значение скорости электронов; Е – напряженность электрического поля; – коэффициент пропорциональности, носящий название подвижности электронов. Применяя формулу (16.7) к электронам в зоне проводимости и к дыркам в валентной зоне, найдем электропроводность:

, (16.8)

где j – плотность электрического тока, – подвижность дырок. Подставляя в (16.8) значение n_c=p_v=n из (16.6), получим:

, (16.9)

где предэкспоненциальный множитель заменен константой D.

Измерим электропроводность σ как функцию температуры и изобразим результаты на графике в полулогарифмическом масштабе:

.

Формула (16.9) показывает, что график должен иметь вид прямой линии с наклоном Е_g/2k. Наклон прямой позволяет, таким образом, определить ширину запрещенной зоны Е_g.

Приведенные соображения верны лишь постольку, поскольку электропроводность полупроводника определяется переходами электронов из валентной зоны в зону проводимости, то есть пока основной вклад в электропроводность вносит собственная проводимость полупроводника. При небольших температурах это обычно не имеет места, так как полупроводники всегда содержат примеси.

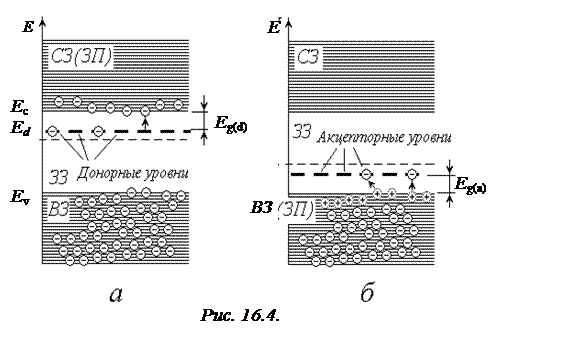Если примеси поставляют существенную часть электронов проводимости и (или) дырок валентной зоны, то мы имеем дело с несобственным полупроводником. Примеси, которые вносят вклад в концентрацию носителей тока, называются донорными, если они поставляют дополнительные электроны в зону проводимости, и акцепторными, когда они поставляют дополнительные дырки в валентную зону (то есть захватывают оттуда электроны). Донорные примеси – это атомы с более высокой валентностью, чем атомы чистого полупроводника (вещество-матрица), а акцепторы – атомы с более низкой валентностью. Самая важная информация о донорных и акцепторных уровнях заключается в том, что они лежат вблизи границ запрещенной зоны. На рис. 16.4 изображены энергетические диаграммы донорного (а) и акцепторного (б) полупроводника.

При тепловом возбуждении гораздо легче вызвать переход электрона в зону проводимости с донорного уровня или на акцепторный уровень из валентной зоны, чем переход через всю запрещенную зону из валентной зоны в зону проводимости. Поэтому при низких температурах именно примеси определяют температурный ход электропроводности полупроводника.

На рис. 16.5 представлена зависимость для полупроводника n-типа (с донорными примесями). Она показывает три области проводимости: n>N_d (собственная проводимость), n≈N_d (область истощения примесей), n<N_d (примесная проводимость). Здесь n – концентрация электронов собственной проводимости, N_d – концентрация электронов примесной проводимости. График имеет два прямолинейных участка, в соответствии с преимущественным вкладом первого или второго слагаемого для данной области температур в формуле (16.10) для удельной электропроводимости такого полупроводника:

. (16.10)

Здесь – энергия активации донорного уровня, имеющего энергию Е_d. В области низких температур угловой коэффициент прямолинейного участка определяется шириной энергетического зазора между донорным уровнем и зоной проводимости. В области высоких температур наклон графика к оси абсцисс определяется шириной запрещённой зоны: .

Итак, наиболее яркая особенность полупроводника состоит в том, что у них в отличие от металлов электросопротивление падает с ростом температуры.

В металлах температурный коэффициент удельного сопротивления

(16.11)

положителен, и его можно считать приближенно постоянным, если интервал изменения температуры достаточно мал. Так, если 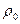есть удельное сопротивление при 0⁰С, а – его значение при t ⁰С, то можно положить

. (16.12)

В классической электронной теории металлов предполагается, что движение электронов подчиняется законам классической механики Ньютона. Электроны проводимости рассматриваются как электронный газ, подобный идеальному газу в молекулярной физике. Предполагается, что причина электрического сопротивления заключается в соударениях электронов с положительными ионами решетки металла.

В действительности же электроны проводимости подчиняются законам квантовой механики, и для них справедлива квантовая статистика – их распределение по энергиям определяется функцией Ферми (16.1). И оказывается, что причина сопротивления чистых металлов – взаимодействие электронов с колебаниями решетки. В квантовой теории кристаллических твердых тел кванты колебаний решетки были названы фононами. Электросопротивление чистых металлов возникает из-за столкновений электронов с фононами. Расчеты показывают, что при высоких температурах (Т>θ_D) ρ~Т, что и наблюдается экспериментально. Здесь θ_D – дебаевская температура металла.