 |
|
Табличными методами минимизации
Они предполагают использование в качестве исходной формулы ту, которая получена с помощью таблиц истинности – совершенную дизъюнктивную нормальную форму логической функции.
Возьмем любую логическую функцию двух аргументов:
| X | Y | F |
Составляем сумму произведений аргументов тех строк, значение функции в которых истинно:
F = 
Составляем таблицу, называемую диаграммой Вейча для функции двух аргументов:
X
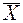
Y 
Записываем единицы в тех ячейках таблицы, которые соответствуют произведениям:

X
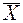
Y 
Единицы, стоящие в ячейках, соприкасающихся сторонами, можно объединить (склеить). При этом вместо двух слагаемых остается одно, имеющее один аргумент, общий для объединяемых ячеек. В данном случае это  . Результат минимизации:
. Результат минимизации:
F =  =
= 
При расстановке слагаемых так:

X
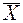
Y 
получаем следующую минимальную форму:
F = X
 При такой расстановке слагаемых:
При такой расстановке слагаемых:

X
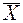
Y 
Имеются два объединения, которые соответствуют следующей минимальной форме:

Если таблица полностью заполнена единицами:
 1 1
| |
X
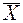
Y 
То после объединения четырех соприкасающихся ячеек получаем следующую минимальную форму:
F = 1
Таким образом, объединять можно по две или по четыре ячейки, оставляя общий для них аргумент.
Диаграмма Вейча для функции трех аргументов имеет вид:

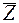 Z
Z 
X
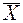
Y 
Здесь тоже можно объединять по две или четыре ячейки, соприкасающиеся сторонами. При этом остаются аргументы, общие для объединенных ячеек:


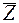 Z
Z 
 1 1
| |||

X
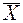
Y 
В этом случае имеются три объединения, образующие следующую минимальную форму:
F = X&Y + Y&Z + 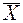 &Z
&Z
При объединении четырех соприкасающихся ячеек остается один общий для них аргумент:

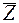 Z
Z 

X
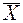
Y 
В этом случае:
F = Y
Можно объединять ячейки, находящиеся на противоположных концах диаграммы:



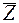 Z
Z 




X
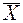
Y 
При этом остаются общие для них аргументы:
F = X& 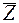
В этом случае:



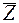 Z
Z 


X
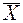
Y 
минимальная форма имеет вид:
F = 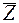
Приложение 2
Системы счисления
Система счисления – совокупность приемов и правил однозначного обозначения чисел с помощью особых символов: 6, 1102, XI.
Символы, при помощи которых записываются числа, называются цифрами, а их совокупность – алфавитом системы счисления.
Количество цифр, составляющих алфавит, называется его размерностью.
Исторически первой системой счисления является односимвольная – использовалась только одна цифра:
•
••
•••
Известны два типа систем счисления:
· непозиционная
· позиционная
В непозиционной системе счисления значение каждой цифры в изображении числа не зависит от ее положения (позиции) в нем. Примером такой системы счисления является римская система счисления, использующая следующие цифры:
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
Римская система счисления является аддитивной – число в ней получается как результат сложения и вычитания базовых цифр:
VI 6
IV 4
В этих числах используются две цифры – I и V. Независимо от того, где они стоят в числах, они обозначают цифры 1 и 5, только в первом случае они складываются, а во втором – вычитаются.
Недостатки непозиционных систем счисления:
· большое количество цифр для изображения числа: MCMXCIII – 1993,
· сложность выполнения арифметических операций.
В позиционных системах счисления значение каждой цифры в изображении числа зависит от ее позиции в нем:
354 = 3×100 + 5×10 + 4×1
В этой записи 3, 5 и 4 являются цифрами десятичной системы счисления, а 100, 10 и 1 – их веса в числе.
Количество цифр, используемых в конкретной системе счисления для изображения числа, называется основанием системы счисления.
В десятичной системе счисления, известной нам с детства, используется десять цифр, поэтому ее основание S=10:
354 = 3×102 + 5×101 + 4×100
Вес цифры в числе можно представить как основание системы счисления в степени, равной номеру разряда числа:
100 вес разряда единиц – номер разряда единиц всегда равен нулю!
101 вес разряда десятков,
102 вес разряда сотен, и так далее.
Нумерация разрядов в целых числах идет справа налево, начиная с нуля. Самый правый разряд называется младшим разрядом числа, а самый левый – старшим.
Представим веса разрядов в виде последовательности чисел, начиная с разряда единиц:
1, 10, 100, 1000, 10000,…
Такая последовательность чисел называется базисом системы счисления. В традиционных системах счисления базис образуют члены геометрической прогрессии. В нетрадиционных системах счисления базис может быть другим:
фибоначчиева:
алфавит – цифры 0, 1
базис – последовательность Фибоначчи: 1, 2, 3, 5, 8, 13, 21,…
факториальная:
базис – последовательность факториалов натуральных чисел: 1!, 2!,3!,…