 |
|
Імпульс тіла – це векторна фізична величина, що є мірою механічного руху і визначається як добуток маси тіла на його швидкість.
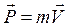
Одиницею імпульсу тіла в СІ є імпульс тіла масою 1 кг, що рухається зі швидкістю 1 м/с: [Р] = 1 кг ∙ 1м/с = 1 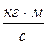
 Числове значення імпульсу тіла розраховують, використовуючи його масу та швидкість.
Числове значення імпульсу тіла розраховують, використовуючи його масу та швидкість.
 Наприклад.
Наприклад.
Яке з двох тіл масами 1 кг та 10 кг, що рухаються зі швидкістю V=10 м/с має більший імпульс і у скільки разів?
 Дано Розв’язування.
Дано Розв’язування.
m1 = 1 кг Імпульс тіл можна визначити за формулою
m2 = 10 кг 
 V = 10 м/с P1 = m1V= 1∙ 10 = 10
V = 10 м/с P1 = m1V= 1∙ 10 = 10 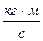
.  - ? Р2 = m2V= 10 ∙ 10 = 100
- ? Р2 = m2V= 10 ∙ 10 = 100 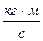

Відповідь: імпульс другого тіла в 10 разів більший.
Закон збереження імпульсу. На початку цього параграфа було зауважено, що імпульс є однією з тих характеристик механічного руху, яка має властивість зберігатися. Тому закон збереження імпульсу розглядають як один із фундаментальних законів не тільки механіки, фізики, а й природи. Встановити цей закон можна, розглянувши пружну взаємодію двох кульок (мал. 3.1.). За третім законом Ньютона сили, що діють на кульки, будуть рівні за модулем і протилежні за напрямом:  . Оскільки взаємодія відбувається деякий час t для обох тіл, то рівними будуть і імпульси сил:
. Оскільки взаємодія відбувається деякий час t для обох тіл, то рівними будуть і імпульси сил:  , підставивши значення імпульсу сили у вираз для імпульсу тіла, отримаємо:
, підставивши значення імпульсу сили у вираз для імпульсу тіла, отримаємо:
 ;
;
 та
та
 .
.
Отже, якщо взаємодія тіл відбувається в замкненій системі, то сума їх імпульсів до взаємодії (  ) дорівнює сумі їх імпульсів після взаємодії (
) дорівнює сумі їх імпульсів після взаємодії (  ).
).
Повний імпульс замкненої системи (сума імпульсів усіх тіл, що взаємодіють у системі) є величиною сталою:
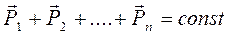
Закон збереження кількості руху (імпульсу) є одним із фундаментальних, основних законів природи. Він є основою багатьох фізичних явищ, проявляється у живій природі і використовується в науці та техніці.
Застосування закону збереження імпульсу дає можливість розв’язувати досить окремі силові взаємодії, без використання основного закону динаміки (другого закону Ньютона).
Наприклад.
Задача 1. Під час запуску моделі ракети (мал. 3.2.) масою 250 г з неї вийшло миттєво 50 г стиснутого повітря зі швидкістю 2 м/с. Знайти швидкість, з якою рухатиметься ракета.
 Дано:
Дано:
М = 250 г = 0,25 кг Розв’язування.
Запишемо закон збереження імпульсу,
m = 50 г = 0,05кг вважаючи систему «модель-повітря» замкнутою.
 Vm = 2 м/с
Vm = 2 м/с 
VМ – ? Якщо вважати, що початкова швидкість моделі ракети V=0, а вісь ОХ спрямувати у напрямі руху ракети, тоді:
0 = (М – m)Vм – mVm;
Отже (М– m)Vм = mVm;

Підставивши значення величин, отримаємо:
Vм =  .
.
Відповідь: модель ракети рухається зі швидкістю 0,5 м/с.
! Головне у цьому параграфі
● Імпульсом або кількістю руху тіла називають векторну фізичну величину, що дорівнює добутку його маси на швидкість.
● Імпульс тіла в СІ вимірюється у 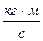 .
.
● Зміна імпульсу тіла пропорційна прикладеній до нього силі і має той самий напрям, що й сила.
● Закон збереження імпульсу виконується у замкненій системі.
● Якщо сума зовнішніх сил дорівнює нулю, то імпульс системи зберігається; тобто сума імпульсів тіл системи до взаємодії дорівнює сумі імпульсів тіл після взаємодії:
 .
.
? Запитання та вправи для самоперевірки
1. Чому імпульс називають кількістю руху?
2. Наведіть приклади ізольованих, замкнених систем.
3. Чи можна вважати замкненою систему «човен-рибалка-поверхня води», «кулька на нитці-повітря», «кулька на підвісі-повітря». Чому?
4. Які із вказаних нижче взаємодій можна не враховувати, вивчаючи рух природного супутника Землі – Місяця: дію Землі; дію Сонця; дію штучного супутника Землі; дію далеких зірок.
5. Чи матиме тіло імпульс, якщо на нього не діє сила?
6. Чи відрізняються за модулем і напрямом імпульс тіла та імпульс сили?
7. Які природні явища підтверджують закон збереження імпульсу?
8. Чому закон збереження імпульсу називають фундаментальним законом природи?
1. Рибалка, маса якого 80 кг, стрибає у нерухомий човен зі швидкістю 3 м/с. З якою швидкістю рухатиметься човен, маса якого 150 кг.
2. Кулька, що рухається зі швидкістю 1 м/с, зустрічається з кулькою, що рухається зі швидкістю 0,5 м/с. Вважаючи удар абсолютно пружним (після взаємодії розміри і форма тіл повністю відновлюються). Знайти швидкості кульок після взаємодії, якщо маса кожної становить 100 г.
3. З якою швидкістю рухатиметься спортсмен, який запускає спис масою 5 кг зі швидкістю 10 м/с під кутом 60° до горизонту. Маса спортсмена 70 кг, метання списа він виконував зі стану спокою.
Реактивний рух
Реактивний рух як прояв закону збереження імпульсу. Приклади реактивного руху в природі. Застосування реактивного руху в техніці та його значення для розвитку космонавтики.
Реактивний рух як прояв закону збереження імпульсу.Реактивний рух можна спостерігати на прикладі роботи приладів шкільної фізичної лабораторії. Одним із них є так зване сегнерове колесо (мал. 3.3). Конічна посудина з водою може вільно обертатися навколо нерухомої осі, а вода витікає з неї через дві загнуті трубки. Якщо трубки закриті, то сила тяжіння, що діє на установку, компенсується силою Архімеда та силою реакції опори. Коли вода вільно витікає через трубки, колесо починає обертатися. Кожна з трубок починає рухатися внаслідок відокремлення (витоку) води у напрямку, протилежному напрямку витікання води. За принципом реактивного руху діє і модель ракети. Накачавши насосом повітря та відкривши клапан, спостерігатимемо реактивний рух моделі внаслідок перерозподілу повітря, яке з деякою швидкістю витікає з ракети. Модель рухається згідно з законом збереження імпульсу у протилежному напрямі.
Експериментуючи з моделлю ракети можна помітити цікаві закономірності, що є суттєвими для використання реактивного руху в техніці. Максимальна швидкість тіла при реактивному русі залежить від його початкової маси та швидкості відділення окремих частин (у розглянутих дослідах – швидкості витікання повітря).
Приклади реактивного руху у природі.Оскільки реактивний рух не потребує для свого підтримання додаткових тіл, крім тих, що утворюють систему (тіло), він є досить поширеними у природі. Окремі живі організми тваринного та рослинного світу використовують закон збереження імпульсу для свого переміщення у просторі. Деякі мешканців морів та океанів можуть створювати реактивні струмені. Так кальмари та каракатиці заповнюють водою порожнисті частини тіла, а потім за допомогою спеціальних м’язів виштовхують її назовні з великою швидкістю. При цьому їм вдається досить швидко переміщуватися.
Деякі сорти городніх культур (наприклад, огірки) після достигання випускають назовні з великою швидкістю своє насіння. Воно рухається в один бік, а сама рослина – в інший (мал. 3.4).
Застосування реактивного руху в техніці та його значення для розвитку космонавтики. Важливість реактивного руху визначається можливістю його використання в умовах, коли відсутній вплив інших тіл. Умовою руху, який ми спостерігаємо зазвичай навколо себе, є наявність сили тертя (рух по поверхні Землі) або сили опору повітря (рух у повітрі), і, відповідно, наявність інших тіл, що й дають можливість рухатися певному тілу.
Реактивний рух може відбуватися і за відсутності навколо тіла, що рухається, інших тіл, тобто, в навколоземному, космічному просторі або вакуумі.
Ідею реактивного руху реалізовано в ракетах – спеціальних пристроях, призначених для польотів за межі нашої планети та дослідження близького і далекого космосу. Загалом ракета складається з двох основних тіл, що утворюють замкнену систему, в якій виконується закон збереження імпульсу – робоча частина та пальне. Робоча частина складається з оболонки, реактивного двигуна, відсіку для обладнання та космонавтів. При цьому основну частину маси ракети складає маса пального (мал. 3.5).
Найпоширенішими сучасними реактивними двигунами є двигуни, що працюють на рідкому паливі. Такі двигуни мають спеціальну камеру згоряння, до якої закачується рідке пальне із зовнішніх резервуарів. За допомогою окислювачів паливо спалюється, в результаті чого утворюються розжарені гази дуже високої температури. Вони створюють тиск на стінки камери згоряння. Задня стінка має спеціальне сопло, через яке розжарений газ виходить назовні. Оскільки сила тиску на передню стінку значно перевищує тиск на задню стінку, створюється реактивна сила тяги, що рухає ракету вперед.
Перші в світі ракети, що були використані для подолання сили земного тяжіння і виведення на орбіту Землі першого штучного супутника та польоту першого космонавта, розроблялися під керівництвом нашого співвітчизника С. П. Корольова (мал. 3.6). Одні з перших рідинних реактивних двигунів були розроблені під керівництвом українського і радянського вченого, академіка В. П. Глушка (мал. 3.7). Реактивні двигуни його конструкції забезпечували надійну роботу космічних апаратів (мал. 3.8).
Важливими показниками сучасної ракети є її максимальна швидкість та маса пального. Максимальна швидкість характеризує можливість ракети подолати, наприклад, силу земного тяжіння (перша космічна швидкість) і вийти на орбіту штучного супутника Землі, вийти на орбіту навколо Сонця (друга космічна швидкість) або залишити межі Сонячної системи.
Швидкість ракети тим більша, чим більше відношення маси палива до маси корпусу ракети, а також, чим більша швидкість витікання газу із сопла реактивного двигуна. Щоб збільшити корисне співвідношення маса пального-корпус, використовують багатоступінчаті ракети (мал. 3.9). Кожна ступінь такої ракети має свій реактивний двигун та баки з пальним, що відкидаються після використання пального в цьому бакові.
Велику роль у дослідженні руху ракети відіграв талановитий російський учений К. Е. Ціолковський (мал. 3.10), який першим запропонував узагальнену формулу для визначення швидкості руху ракети («формула ракети»), ідею багатоступінчатих ракет тощо. Наш співвітчизник Ю. В. Кондратюк (О. Г. Шаргей) (мал. 3.11) незалежно від К. Е. Ціолковського іншими методами отримав рівняння руху ракети, що стало підтвердженням об’єктивного характеру розвитку вчення про реактивні пристрої. В історії світової астронавтики увійшла і «зоряна траса» Ю. В. Кондратюка – схема гравітаційного маневру для польоту на інші тіла нашої планетної системи (мал. 3.12). Цю схему було вдало використано американськими астронавтами під час польоту на природний супутник Землі – Місяць.
Нині наша країна є космічною державою, однією з небагатьох, що проектують і виготовляють ракети – носії для виведення на орбіту штучних супутників, космічних кораблів на станції. Вітчизняні реактивні носії «Зеніт» щороку здійснюють польоти з наземних та морських космодромів.
! Головне у цьому параграфі
• Реактивний рух є проявом закону збереження імпульсу.
• Система, що здійснює реактивний рух, не потребує взаємодії з іншими тілами, крім тих, що входять до неї. Тому вона забезпечує можливість переміщення у навколоземному просторі.
? Запитання та вправи для самоперевірки
1. Яка важлива особливість реактивного руху забезпечує його широке використання в сучасній техніці?
2. Які основні складові сучасної ракети?
3. Які характеристики ракети визначають її максимальну швидкість?
4. Яким чином створюється реактивна сила у реактивному двигуні?
5. Яким чином вирішують питання необхідності збільшення співвідношення корисної маси до маси оболонки ракети?
* Запропонуйте власну схему космічної ракети майбутнього. Розкрийте внесок вітчизняних учених і конструкторів до справи освоєння космосу.