 |
|
Метод простых итераций
Заменим уравнение 
эквивалентным ему уравнением 
Это преобразование можно выполнить не единственным образом.
Функция 
должна быть по крайней мере определена и дифференцируема на 
Зададим какое-либо начальное приближение к корню 
Дальнейшие приближения будем вычислять по итерационной формуле
Если 
стремится к некоторому значению 
, то - предел последовательности.
есть корень уравнения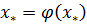 
.
Исследуем, есть ли ограничения на сходимость.
Вычтем из 
уравнение 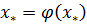и разложим 
в ряд Тейлора в окрестности точки 
:
Если всюду на некотором отрезке 
выполнимо
(достаточное условие сходимости)
то получаемая последовательность 
сходится при любом начальном приближении 
, т.к. тогда
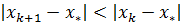
Если 
, но вдали от корня 
, то итерации будут сходиться, если начальное приближение выбрано достижимо близко к корню.
Если , то в силу непрерывности функции 
будет больше единицы и в некоторой окрестности корня.
В этом случае итерации расходятся.
Билет 8
1. Решение нелинейного уравнения.
2. Этапы решения нелинейного уравнения.
3. Модифицированный метод простых итераций.
Модифицированный метод простых итераций
Этот метод позволяет решение, даже если
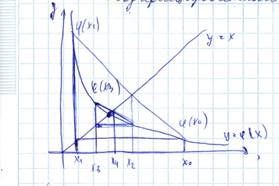Первое приближение находится по методу простых итераций
Через точки 
и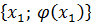 
проводим прямую.
Находим точку пересечения этой прямой с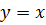 
.
Абсциссу точки пересечения обозначим, как 
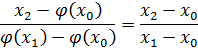
– на нечётном шаге
– на чётном шаге
Билет 9
1. Решение нелинейного уравнения.
2. Этапы решения нелинейного уравнения.
3. Метод Чебышева.
Метод Чебышева
Пусть уравнение 
на имеет корень x. Пусть 
. Функция имеет обратную функцию 
и 
Тогда
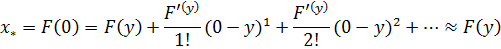
Можно записать, что
С……… 
итерационная схема будет иметь вид:
– формула Чебышева
Найдём производные от обратной функции
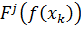
Дифференцируем соотношение
Дифференцируем соотношение ещё раз
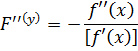
Билет 10
1. Решение систем нелинейных уравнений.
2. Метод простых итераций.