Главная | Обратная связь

Определение упругого перемещения переднего конца шпинделя

 

1. Суммарное упругое перемещение переднего конца шпинделя определяется по формуле

где - перемещения переднего конца шпинделя в плоскостях XZ и XY

2. Упругое перемещение переднего конца шпинделя при расчетной схеме с приводным элементом на межопорной части шпинделя может определяться в двух плоскостях – по и по формуле

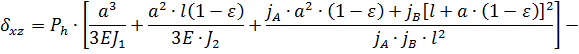
где , и – силы резания, Н: , принимаем

принимаем ;

– вылет переднего конца шпинделя, ;

модуль упругости материала шпинделя, МПа

– средний осевой момент инерции сечения консоли переднего конца шпинделя, ;

– средний осевой момент инерции сечения шпинделя между опорами,

расстояние между передней и задней опорами шпинделя, мм;

коэффициент защемления в передней опоре; для данной схемы шпиндельного узла и типов установленных подшипников; принимаем

радиальная жесткость передней опоры, Н/мм;

– радиальная жесткость задней опоры, Н/мм;

– расстояние от приводного элемента на межопорной части шпинделя до передней опоры, мм:

3. Средний осевой момент инерции сечения консоли переднего конца шпинделя (рисунок 7.2) определяется по формуле

где средний диаметр шеек консоли шпинделя, мм;

- средний диаметр отверстий консоли шпинделя, мм.

Средний диаметр шеек консоли шпинделя определяется по формуле

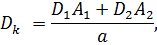
где – диаметры шеек консоли шпинделя, мм:

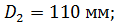
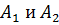– соответствующие длины шеек шпинделя, мм: ,

,

– длина консоли шпинделя, мм: .

 

Средний диаметр отверстий консоли шпинделя определяется по формуле

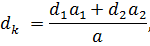
где – диаметры отверстий консоли шпинделя, мм:

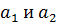– соответствующие длины отверстий шпинделя, мм: ,

,

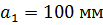– длина консоли шпинделя, мм: .

Средний осевой момент инерции сечения консоли переднего конца шпинделя

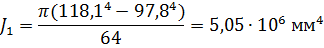
4. Средний осевой момент инерции сечения шпинделя в пролете между опорами (рисунок 7.2) определяется по формуле

где - средний диаметр шеек межопорной части шпинделя, мм;

- диаметр отверстий шпинделя в межопорной части, мм;

Средний диаметр шеек межопорной части шпинделя определяется по формуле

где , , , , 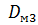– диаметры шеек межопорной части шпинделя, мм:

– соответствующие длины шеек межопорной части шпинделя, мм;

– длина межопорной части шпинделя, мм:

Средний диаметр отверстия межопорной части шпинделя определяется по формуле

где 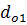, , , , – диаметры отверстий в межопорной части шпинделя, мм:

– соответствующие длины отверстий в межопорной части шпинделя, мм:

– длина межопорной части шпинделя, мм:

 

 

Средний осевой момент инерции сечения шпинделя в пролете между опорами:

5. Радиальная жесткость передней опоры состоит из суммы радиальных жесткостей радиального двухрядного роликового подшипника с коническим посадочным отверстием и упорно-радиального подшипника с углом контакта 60°, зависит от их диаметра посадочного отверстия и определяется по графику.

Для радиального двухрядного роликового подшипника с коническим посадочным отверстием радиальная жесткость выбирается по графику в зависимости от диаметра посадочного отверстия. Для диаметра посадочного отверстия радиальная жесткость равна

Осевая жесткость упорно-радиального шарикового подшипника с углом контакта 60°рассчитывается по формуле

где 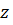– количество тел качения в подшипнике, ,

- диаметр тел качения, мм;

сила натяга, Н: ,

– коэффициент, учитывающий погрешность изготовления,

Радиальная жесткость упорно-радиального шарикового подшипника с углом контакта 60°рассчитывается по формуле

Радиальная жесткость передней опоры равна

Радиальная жесткость задней опоры рассчитывается, как жесткость комплексной опоры по формуле:

где – осевая жесткость комплексной опоры, рассчитывается для данной опоры по формуле:

где - сила натяга, Н. Определяется по таблице в зависимости от серии и диаметра подшипника

– динамическая грузоподъемность подшипника,

Радиальная жесткость задней опоры

 

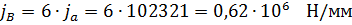
6. Перемещение переднего конца шпинделя в плоскости XY

7. Перемещение переднего конца шпинделя в плоскости XZ

8. Общее упругое перемещение переднего конца шпинделя

Допустимое перемещение переднего конца шпинделя

– длина межопорной части шпинделя, мм: