 |
|
Расчетные диаметры передач и их модули
4.3.1 Расчет цилиндрической прямозубой передачи 
и косозубых передач 
, 
, 
групповой передачи
· Исходные данные:
Расчет ведется по наиболее нагруженной передаче по следующим исходным данным:
1. Расчетный крутящий момент на втором валу привода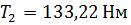 
2. Число зубьев шестерни 
3. Число зубьев колеса 
4. Передаточное число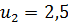 
· Выбор материала зубчатых колес и вида термической обработки:
В качестве материала для зубчатых колес назначается сталь 25ХГМ, которая отвечает необходимым техническим и эксплуатационным требованиям. В качестве термической обработки выбирается нитроцементация с закалкой, позволяющая получить твердость зубьев 58-60 HRC.
· Проектный расчет прямозубой передачи 
групповой передачи на контактную выносливость зубьев:
Диаметр начальной окружности шестерни 
рассчитывается по формуле
где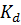 
– вспомогательный коэффициент; для прямозубых передач 
;
– расчетный крутящий момент на втором валу привода, 
– коэффициент нагрузки для шестерни, равный 1,3-1,5; принимается 
– передаточное число передачи: 
– отношение рабочей ширины венца передачи к начальному диаметру шестерни: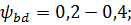 
- допускаемое контактное напряжение, МПа
Допускаемое контактное напряжение для косозубых передач рассчитывается по формуле
где 
- базовый передел контактной выносливости поверхностей зубьев, соответствующий базовому числу циклов перемены напряжений: 
;
– коэффициент безопасности: 
Коэффициент отношения рабочей ширины венца передачи к начальному диаметру шестерни может приниматься в пределах 
или определяться по формуле
где – отношение рабочей ширины венца передачи к начальному диаметру шестерни;
– отношение рабочей ширины венца передачи к модулю: 
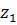– число зубьев шестерни
Полученное значение отношения рабочей ширины венца передачи к начальному диаметру шестерни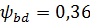 
и находится в допускаемых пределах.
Диаметр начальной окружности шестерни
Модуль передачи определяется из условия расчета на контактную выносливость зубьев по рассчитанному значению диаметра начальной окружности шестерни по формуле
где 
– диаметр начальной окружности шестерни, мм: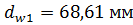 
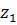– число зубьев шестерни: 
· Проектный расчет прямозубой передачи групповой передачи на выносливость зубьев при изгибе:
Модуль передачи при проектном расчете зубьев на изгибную выносливость рассчитывается по формуле
где 
– вспомогательный коэффициент, зависящий от коэффициента осевого перекрытия: 
;
– расчетный крутящий момент на втором валу привода, 
– коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца: 
;
– коэффициент, учитывающий форму зуба: 
;
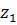– число зубьев шестерни: ;
– значение отношения рабочей ширины венца передачи к модулю; 
– допускаемое напряжение зубьев при изгибе, МПа.
Допускаемое напряжение зубьев при изгибе рассчитывается по формуле
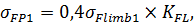
где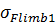 
– предел выносливости материала зубьев,МПа: 
– коэффициент режима нагрузки и долговечности: 
Модуль передачи при проектном расчете на изгибную выносливость
· Определение модуля прямозубой передачи групповой передачи
По контактной выносливости модуль передачи должен быть 
мм, а по выносливости зубьев при изгибе 
мм. Следует принимать стандартное большее значение модуля 
· Расчет геометрических характеристик параметров передач групповой передачи
Геометрические параметры передач определяются по формулам:
1) Делительные диаметры шестерни и колеса 
:
2) Диаметры окружностей вершин зубьев шестерни и колеса :
3) Диаметры окружностей впадин зубьев шестерни и колеса :
4) Ширина зубчатого венца шестерни и колеса :
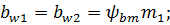
5) Межосевое расстояние:
6) Корректировка косозубых передач 
групповой передачи:
Межосевое расстояние для косозубой передачи определяется по формуле
где 
– угол наклона зубьев; принимается 8-16°; предварительно принимаем 
– нормальный модуль косозубых передач, 
Т.к. в групповой передаче есть и косозубые, и прямозубые передачи, то должно выполняться равенство
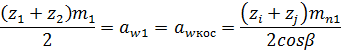
Из данного неравенства находим сумму зубьев косозубой передачи.
Полученное значение 
округляем до большего целого числа, принимаем 
Согласовываем округленное суммарное число зубьев с таблицей зубчатых передач, чтобы обеспечить передаточные числа всех передач в групповой передаче.
Определяем действительный угол наклона для косозубых передач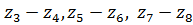 
групповой передачи:
Определяем числа зубьев шестерен и колес для косозубых передач групповой передачи:
; 
; 
; 
7) Делительные диаметры косозубых передач групповой передачи:
8) 
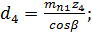
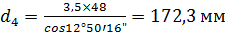
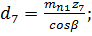
9) Диаметры окружностей вершин зубьев косозубых передач 
групповой передачи:
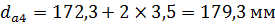
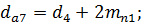
10) Диаметры окружностей впадин зубьев косозубых передач
групповой передачи:
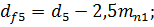
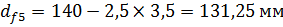
11) Ширина зубчатого венца:
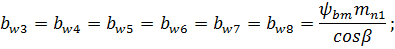
Результаты вычислений сведены в таблицу 4.1.
Таблица 4.1 – Геометрические параметры зубчатой передачи
| Наименование параметра | Обозначение | Значение |
| 1. Передаточное число и отношение |
| 2,5 1,57 1,57 |
| 2. Модуль, мм | 
| 3,5 |
| 3. Модуль нормальный, мм |
| 3,5 |
| 4. Число зубьев колес |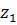
| |
| 5. Делительный диаметр колес, мм | 
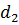
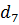
| 80,5
199,5
172,3
172,3
107,7
|
| 6. Диаметр окружности вершин зубьев колес, мм | 
| 87,5
206,5
|
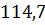
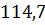
| 7. Диаметр окружности впадин зубьев колеса, мм | 
| 71,75
190,75
|
| 8. Межосевое расстояние, мм | 
| |
| 9. Ширина зубчатого венца, мм |  =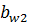 
|
4.3.2 Расчет постоянной цилиндрической прямозубой передачи 
· Исходные данные:
1. Расчетный крутящий момент на третьем валу привода 
2. Число зубьев шестерни 
3. Число зубьев колеса 
4. Передаточное число 
· Выбор материала зубчатых колес и вида термической обработки
В качестве материала для зубчатых колес назначается сталь 40Х, которая отвечает необходимым техническим и эксплуатационным требованиям. В качестве термической обработки выбирается закалка ТВЧ, позволяющая получить твердость зубьев 48-52 HRC.
Проектный расчет постоянной цилиндрической прямозубой передачи 
на контактную выносливость зубьев
Диаметр начальной окружности шестерни 
рассчитывается по формуле
где 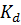– вспомогательный коэффициент; для прямозубых передач ;
– расчетный крутящий момент на третьем валу привода, 
– коэффициент нагрузки для шестерни, равный 1,3-1,5; принимается
– передаточное число передачи: 
– отношение рабочей ширины венца передачи к начальному диаметру шестерни: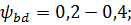
- допускаемое контактное напряжение, МПа
Допускаемое контактное напряжение для косозубых передач рассчитывается по формуле
где 
- базовый передел контактной выносливости поверхностей зубьев, соответствующий базовому числу циклов перемены напряжений: 
;
– коэффициент безопасности:
Коэффициент отношения рабочей ширины венца передачи к начальному диаметру шестерни может приниматься в пределах или определяться по формуле
где – отношение рабочей ширины венца передачи к начальному диаметру шестерни;
– отношение рабочей ширины венца передачи к модулю:
– число зубьев шестерни
Полученное значение отношения рабочей ширины венца передачи к начальному диаметру шестерни 
и находится в допускаемых пределах.
Диаметр начальной окружности шестерни
Модуль передачи определяется из условия расчета на контактную выносливость зубьев по рассчитанному значению диаметра начальной окружности шестерни по формуле
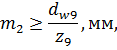
где 
– диаметр начальной окружности шестерни, мм: 
– число зубьев шестерни: 
· Проектный расчет постоянной цилиндрической прямозубой передачи 
на выносливость зубьев при изгибе
Модуль передачи при проектном расчете зубьев на изгибную выносливость рассчитывается по формуле
где – вспомогательный коэффициент, зависящий от коэффициента осевого перекрытия: ;
– расчетный крутящий момент на третьем валу привода, 
– коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца: ;
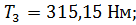
– коэффициент, учитывающий форму зуба: 
;
– число зубьев шестерни: ;
– значение отношения рабочей ширины венца передачи к модулю;
– допускаемое напряжение зубьев при изгибе, МПа.
Допускаемое напряжение зубьев при изгибе рассчитывается по формуле
где 
– предел выносливости материала зубьев,МПа: 
– коэффициент режима нагрузки и долговечности:
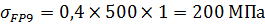
Модуль передачи при проектном расчете на изгибную выносливость
· Определение модуля цилиндрической прямозубой передачи 
По контактной выносливости модуль передачи должен быть 
мм, а по выносливости зубьев при изгибе 
мм. Следует принимать стандартное большее значение модуля 
· Расчет геометрических характеристик параметров цилиндрической прямозубой передачи
Геометрические параметры прямозубой передачи определяются по формулам:
1) Делительные диаметры шестерни и колеса 
:
2) Диаметры окружностей вершин зубьев шестерни и колеса:
3) Диаметры окружностей впадин зубьев шестерни и колеса:
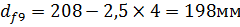
4) Межосевое расстояние:
5) Ширина зубчатого венца:
Результаты вычислений сведены в таблицу 4.2.
Таблица 4.2 – Геометрические параметры зубчатой передачи
| Наименование параметра | Обозначение | Значение |
| 1. Передаточное число |
| 1,27 |
| 2. Модуль нормальный, мм | 
| |
| 3. Число зубьев шестерни |
| |
| 4. Число зубьев колеса |
| |
| 5. Делительный диаметр шестерни, мм | 
| |
| 6. Делительный диаметр колеса, мм | 
| |
| 7. Диаметр окружности вершин зубьев шестерни, мм | 
| |
| 8. Диаметр окружности вершин зубьев колеса, мм | 
| |
| 9. Диаметр окружности впадин зубьев шестерни, мм | 
| |
| 10. Диаметр окружности впадин зубьев колеса, мм |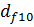 
| |
| 11. Межосевое расстояние, мм | 
| |
| 12. Ширина зубчатого венца, мм | 
|
4.3.3 Расчет поликлиновой ременной передачи 
· Исходные данные:
– крутящий момент на валу электродвигателя, Нм;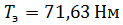 
Передаточное число 
· Сечение ремня:
Сечение ремня принимается по крутящему моменту электродвигателя. Для крутящего момента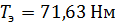 
принимаем сечение ремня Л. Также для такого крутящего момента минимальный диаметр 
· Диаметр меньшего шкива:
Оптимальный диаметр меньшего шкива следует принимать больше или равным 
для повышения долговечности ремня и КПД передачи.
При 
диаметр меньшего шкива рассчитывается по формуле:
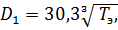
где – крутящий момент на валу электродвигателя, Нм;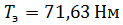
Принимаем стандартное значение диаметра шкива 
· Диаметр большего шкива
Диаметр большего шкива рассчитывается по формуле:
где 
– диаметр меньшего шкива, мм; 
– передаточное число,
· Скорость ремня:
Скорость ремня рассчитывается по формуле:
где – диаметр меньшего шкива, мм;
– номинальная частота электродвигателя,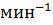 
; 
· Межосевое расстояние:
Минимальное межосевое расстояние определяется по формуле:
где 
- высота клина поликлинового ремня, принимается по таблице, 
мм
Принимаем 
· Длина ремня:
Длина ремня определяется по формуле:
где 
– предварительно принятое межосевое расстояние, 
Принимаем длину ремня из стандартного ряда 
1120 мм
· Уточненное межосевое расстояние:
Уточняем межосевое расстояние после принятия стандартной длины ремня по формуле:
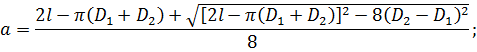
· Угол обхвата α:
Угол обхвата на малом шкиве рассчитывается по формуле:
где – уточненное межосевое расстояние, 
· Допускаемая мощность на один ремень с 10 ребрами:
Допускаемая мощность на один ремень с 10 ребрами в реальных условиях рассчитывается по формуле:
где 
– исходная мощность, выбирается по таблице 
– коэффициент угла обхвата, 
– коэффициент, учитывающий влияние на долговечность длины ремня, принимается 
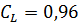
– коэффициент динамичности и режима нагрузки, принимается 
поправка, учитывающая влияние изгиба на большом шкиве:
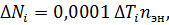
где 
– поправка к моменту на быстроходном валу, 
Нм
– номинальная частота электродвигателя, ;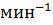
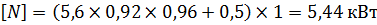
· Число ребер Z:
Число ребер Z поликлинового ремня рассчитывается по формуле:
где 
– передаваемая мощность, 
– Допускаемая мощность на один ремень с 10 ребрами,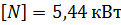 
Принимаем ремень с числом ребер 
· Сила предварительного натяжения ремня с числом зубьев Z:
где – передаваемая мощность,
– коэффициент угла обхвата,
Z – число ребер, Z=14
– масса 1 м ремня с 10 ребрами, 
кг/м
– коэффициент динамичности и режима нагрузки, принимается
· Сила, действующая на валы:
Сила, действующая на валы, выражается через 
· Геометрические параметры шкивов:
Расчетные диаметры шкивов:
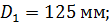
Наружные диаметры шкивов:
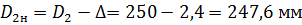
Ширина шкивов: 
Рисунок 4.2 – Сечение применяемого ремня
4.3.4 Расчет постоянной конической прямозубой передачи 
· Исходные данные
1. Расчетный крутящий момент на третьем валу привода 
2. Число зубьев шестерни 
3. Число зубьев колеса 
4. Передаточное число . Передаточное число принимается таким же, как и в зубчатой передаче с целью обеспечить одинаковые диапазоны регулирования частот вращения вертикального и горизонтального шпинделей.
· Выбор материала зубчатых колес и вида термической обработки
В качестве материала для зубчатых колес назначается сталь 25ХГМ, которая отвечает необходимым техническим и эксплуатационным требованиям. В качестве термической обработки выбирается нитроцементация с закалкой, позволяющая получить твердость зубьев 58-60 HRC.
· Проектный расчет конической прямозубой передачи 
на контактную выносливость зубьев
Диаметр средний диаметр делительный шестерни 
рассчитывается по формуле
где 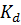– вспомогательный коэффициент; для прямозубых передач ;
– расчетный крутящий момент на пятом валу привода, 
– коэффициент нагрузки для шестерни, принимается по графику исходя из величины 
, где 
. Принимаем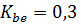 
и
– передаточное число передачи:
– отношение рабочей ширины венца передачи к начальному диаметру шестерни: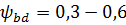 
и рассчитывается по формуле:
где 
– угол делительного конуса,
,
Принимаем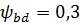 
- допускаемое контактное напряжение, МПа
Допускаемое контактное напряжение для косозубых передач рассчитывается по формуле
где 
- базовый передел контактной выносливости поверхностей зубьев, соответствующий базовому числу циклов перемены напряжений: 
;
– коэффициент безопасности:
Средний окружной модуль передачи определяется из условия расчета на контактную выносливость зубьев по рассчитанному значению среднего делительного диаметра шестерни по формуле
где 
– диаметр начальной окружности шестерни, мм: 
– число зубьев шестерни: 
· Проектный расчет конической прямозубой передачи на выносливость зубьев при изгибе
Средний окружной модуль передачи при проектном расчете зубьев на изгибную выносливость рассчитывается по формуле
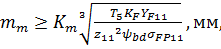
где – вспомогательный коэффициент, зависящий от коэффициента осевого перекрытия: 
;
– расчетный крутящий момент на пятом валу привода,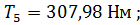 
– коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца, принимается по графику исходя из величины ,
– коэффициент, учитывающий форму зуба, принимается по графику исходя из величины эквивалентного числа зубьев 
. Принимаем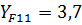 
– число зубьев шестерни: 
;
– допускаемое напряжение зубьев при изгибе, МПа.
Допускаемое напряжение зубьев при изгибе рассчитывается по формуле
где 
– предел выносливости материала зубьев,МПа: 
; – коэффициент режима нагрузки и долговечности:
Модуль передачи при проектном расчете на изгибную выносливость
· Определение модуля конической прямозубой передачи 
По контактной выносливости Средний окружной модуль передачи должен быть 
мм, а по выносливости зубьев при изгибе 
мм. Следует принимать значение среднего окружного модуля 
Рассчитываем внешний окружной модуль, который стандартизуется:
Принимаем стандартное значение внешнего окружного модуля 
.
· Расчет геометрических характеристик параметров конической прямозубой передачи
Геометрические параметры конической прямозубой передачи определяются по формулам:
1) Число зубьев плоского колеса:
2) Внешнее конусное расстояние
3) Углы делительных конусов:
4) Внешние делительные диаметры шестерни и колеса
5) Внешние диаметры вершин зубьев шестерни и колеса
6) Внешние диаметры впадин зубьев шестерни и колеса
7) Ширина венца зубчатого колеса
8) Среднее конусное расстояние
9) Средний окружной модуль
10) Средние делительные диаметры шестерни и колеса:
Результаты вычислений сведены в таблицу 4.3.
Таблица 4.3 – Геометрические параметры зубчатой передачи
| Наименование параметра | Обозначение | Значение |
| 1. Передаточное число |
| 1,27 |
| 2. Число зубьев плоского колеса |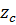 
| 
|
| 3. Число зубьев шестерни |
| |
| 4. Число зубьев колеса | 
| |
| 5. Углы делительных конусов, град | 
| 38,04 51,96 |
| 6. Внешнее конусное расстояние, мм | 
| 142,42 |
| 7. Внешние делительные диаметры шестерни и колеса, мм | 
| |
| 8. Внешние диаметры вершин зубьев шестерни и колеса, мм | 
| 182,3 228,92 |
| 9. Внешние диаметры впадин зубьев шестерни и колеса, мм | 
| 168,43 218,08 |
| 10. Ширина венца зубчатого колеса, мм |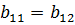 
| |
| 11. Среднее конусное расстояние, мм | 
| 121,42 |
| 12. Средний окружной модуль, мм | 
| 3,4 |
| 13. Средние делительные диаметры шестерни и колеса, мм |
| 149,6 190,4 |