 |
|
Автокорреляция уровней временного ряда
При наличии в динамическом ряде трендовой и циклической компонент значения последующего уровня ряда зависят от предыдущих. Это корреляционная зависимость между последовательными уровнями одного и того же ряда, сдвинутыми на определенный промежуток времени L – лаг, называется автокорреляцией уровней ряда. Количественно её можно измерить с помощью линейного коэффициента корреляции. Лаг определяет порядок коэффициента автокорреляции. В частности, при 
получаем коэффициент автокорреляции первого порядка, который характеризует тесноту связи между уровнями 
и 
:
, где 
; 
.
Аналогично можно определить коэффициенты автокорреляции второго т более высоких порядков. В общем случае для рядов 
и 
, где 
, 
коэффициент автокорреляции определяется формулой:
, где
- средний уровень ряда 
,
- средний уровень ряда 
.
Последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков называют автокорреляционной функцией (АКФ) временного ряда. Одним из наиболее распространенных методов выявления во временном ряде наличия (или отсутствия) трендовой и сезонной компонент является построение графиков АКФ и частной автокорреляционной функции (ЧАКФ). Графиком АКФ является коррелограмма. Она отражает либо АКФ, либо коэффициенты корреляции для последовательности лагов из определенного диапазона. Если АКФ – это функция оценки коэффициента автокорреляции в зависимости от величины временного лага между исследуемыми рядами, то ЧАКФ – это функция, дающая углубленное понятие обычной АКФ. В ЧАКФ устраняется корреляционная зависимость между наблюдениями внутри лагов. Для обеспечения статистической достоверности коэффициентов автокорреляции их максимальный порядок должен быть не больше 
/4.
Рассчитав несколько коэффициентов автокорреляции, можно определить лаг, при котором автокорреляция наиболее высокая. Тем самым выявляется структура временного ряда. Если наиболее высоким оказывается значение коэффициента автокорреляции первого порядка, то исследуемый ряд содержит только трендовую компоненту. Если же наиболее высоким оказался коэффициент автокорреляции порядка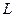 
, то помимо тенденции ряд содержит колебания с периодом 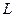. В случае, если ни один из коэффициентов автокорреляции не является значимым, то либо ряд не содержит трендовой и циклической компонент, либо ряд содержит сильную нелинейную тенденцию. В первом случае уровень ряда определяется только случайной компонентой, а во втором – для выявления нелинейной тенденции необходимо проводить дополнительный анализ. Наконец, если колебания временного ряда вызваны воздействием иррегулярной компоненты, то имеет место модель случайного тренда.