 |
|
Аналитическое выравнивание
Среди известных способов определения типа тенденции следует выделить: качественный анализ изучаемого процесса, построение и визуальный анализ графика зависимости уровней ряда от времени, расчет некоторых основных показателей динамики, в частности, коэффициентов автокорреляции уровней ряда. Путем сравнения коэффициентов автокорреляции первого порядка, рассчитанных по исходным и преобразованным уровням ряда, можно определить тип тенденции. Если временной ряд имеет линейную тенденцию, то его соседние уровни тесно коррелируют между собой. В этом случае 
исходного ряда должен быть высоким. Чем сильнее выражена нелинейная тенденция в изучаемом временном ряде, тем в большей степени будут различаться значения указанных коэффициентов.
Наиболее распространенным способом моделирования тенденции временного ряда является построение аналитической функции, характеризующей зависимость уровней ряда от времени, или тренда. Этот способ называют аналитическим выравниванием временного ряда. Суть метода заключается в замене эмпирических откликов 
аналитическими 
. Каждый фактический отклик определяется 
, где 
- трендовая составляющая, а 
- случайная составляющая, описывающая колебания откликов вокруг тренда. Алгоритм аналитического сглаживания включает в себя:
1. выбор функции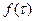 
;
2. определение параметров функции;
3. расчет по найденному уравнению теоретических откликов .
Поскольку зависимость от времени может принимать разные формы, для ее формализации можно использовать различные виды функций. В аналитическом выравнивании для построения трендов зачастую применяются линейная, степенная, показательная, гиперболическая функции, Фурье-функция и полиномы различных степеней. В качестве объясняющей переменной выступает время, а в качестве эндогенной – фактические уровни временного ряда. Параметры каждого из перечисленных трендов можно определить традиционным методом наименьших квадратов (МНК). Для нелинейных трендов предварительно проводят стандартную процедуру их линеаризации. Выбор нужной функции осуществляется на основе графического изображения исходного ряда. Критерием отбора наилучшей формы тренда служит наибольшее значение скорректированного коэффициента детерминации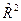 
и наименьшая величина средней ошибки аппроксимации.
При выборе вида функции тренда используют метод конечных разностей. Обязательным условием применения данного подхода является равенство интервалов между уровнями ряда. Конечными разностями первого порядка являются разности между последовательными уровнями ряда: 
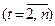. Конечными разностями второго порядка являются разности между последовательными уровнями ряда первого порядка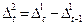 
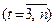. Аналогично определяются конечные разности 
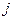-го порядка:
.
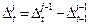
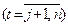Если общая тенденция выражается линейным уравнением, то конечные разности первого порядка постоянны, а разности 2-го порядка равны нулю. Если примерно постоянными оказываются темпы роста, то для сглаживания используется показательная функция. Если же общая тенденция выражается параболой 2-го порядка, то постоянны конечные разности второго порядка, а разности 3-го - нулевые. В случае, если ряд сложно описать одной функцией, его разбивают на части, описывая каждую часть своей функцией. Если ряд удается сгладить по разным функциям, то при выборе наилучшей функции тренда более приемлема функция с наименьшей суммой 
.