 |
|
Модели с распределенным лагом и авторегрессии
Эконометрическое моделирование осуществляется с применением моделей, содержащих не только текущие, но и лаговые значения переменных. Модели с распределенным лагом – это ДЭМ, в которых содержатся не только текущие, но и лаговые значения факторных переменных. Вводятся новые показатели: весовые коэффициенты, средний и медианный лаги. Применение МНК к моделям с распределенным лагом в большинстве случаев неприемлемо, поэтому на практике оценку параметров таких ДЭМ проводят с помощью специальных методов: метод Алмон, метод Койка. Лаги Алмон используют для описания модели с распределенным лагом, имеющей полиномиальную структуру лага и конечную величину лага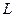 
. Метод Койка обычно применяется, во-первых, если величина лага – бесконечно большая, а во-вторых, в предположении геометрической структуры лага. Иначе говоря, метод Койка опирается на предположение о том, что коэффициенты при лаговых значениях объясняющей переменной убывают в геометрической прогрессии.
К моделям авторегрессии неприемлемо применение МНК, так как нарушается первая предпосылка нормальной линейной модели регрессии, а именно, одна из объясняющих переменных 
частично зависит от случайной составляющей 
. Это приводит к получению смещённой оценки параметра при переменной . Коэффициент регрессии 
в моделях характеризует краткосрочное изменение 
под влиянием изменения 
на единицу своего измерения. Его называют краткосрочным мультипликатором. Коэффициент 
характеризует изменения в момент времени 
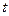под воздействием своего изменения в предшествующий момент времени 
. Произведение коэффициентов 
называют промежуточным мультипликатором. Он характеризует общее абсолютное изменение результата в момент 
. Показатель 
называют долгосрочным мультипликатором. Он характеризует общее абсолютное изменение в долгосрочном периоде. Практически во все модели авторегрессии вводят условие стабильности 
.
Для оценивания параметров уравнения моделей авторегрессии используют и метод инструментальных переменных:
1. переменную заменяют на новую переменную, которая должна тесно коррелировать с , но не должна коррелировать со случайной составляющей ;
2. оценивают регрессию с новой инструментальной переменой с помощью МНК.