Главная | Обратная связь

Знакочередующиеся ряды. Признак Лейбница. Примеры условно и абсолютно сходящихся рядов

ЗНАКОПеременныЕ ряды

Знакопеременные ряды. Абсолютная сходимость, условная сходимость

 

Определение. Знакопеременным рядом называется ряд, членами которого являются вещественные числа произвольного знака.

Знакопеременный ряд будем записывать в виде:

u₁ + u₂ + . . . + u_n +. . . = 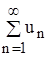, считая, что числа u₁, u₂, … могут быть и положительными, и отрицательными.

Достаточный признак сходимости знакопеременного ряда.

Теорема.Знакопеременный ряд u₁ + u₂ + . . . + u_n +. . . (1) сходится, если сходится ряд |u₁| + |u₂| + . . . + |u_n| +. . . (2), составленный из абсолютных величин членов ряда (1).

Доказательство.

Очевидно, что 0 £ u_n + | u_n| £ 2 |u_n| . (3)

Здесь величина 2 |u_n| представляет собой общий член сходящегося ряда 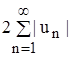, а величина u_n + |u_n| есть общий член ряда 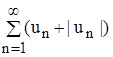. (4)

По признаку сравнения из неравенства (3) следует сходимость ряда (4). Из сходимости рядов 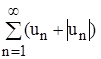и следует, что будет сходиться и ряд, членами которого являются разности соответствующих членов этих рядов, т. е. ряд

,

 

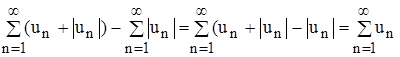а это и есть данный ряд. Теорема доказана.

Вывод.Таким образом, для сходимости знакопеременного ряда достаточно сходимости ряда, составленного из модулей его членов.

Знакочередующиеся ряды. Признак Лейбница. Примеры условно и абсолютно сходящихся рядов

Рассмотрим знакочередующиеся ряды, которые являются частным случаем знакопеременных рядов.

Определение. Ряд, у которого любые стоящие рядом члены имеют противоположные знаки, называются знакочередующимися.

Его можно записать в виде:

u₁ – u₂ + u₃ – u₄ + . . . (–1)ⁿ⁺¹u_n +. . . , где u_n > 0, при n = 1, 2. . .

Для знакочередующихся рядов имеет место простой достаточный признак сходимости – признак Лейбница (Лейбниц Готфрид Вильгельм 1646-1716).

Признак Лейбница. Если абсолютные величины членов знакочередующегося ряда

u₁ – u₂ + u₃ – u₄ + . . . (–1)ⁿ⁺¹u_n +. . . , (5)

монотонно убывают, т. е.

u₁ ³ u₂ ³ u₃ ³ . . . , (6)

и общий член u_n при неограниченном возрастании n стремится к нулю:

то ряд сходится и его сумма не превосходит величины первого слагаемого.

Доказательство.

Требуется доказать, что ряд (5) сходится, т.е. существует .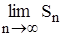

Докажем существование пределаS_n, разобрав 2 случая, когда:

1) n – число четное,

2) n – число нечетное.

Итак, 1) n – число четное. Тогда частичную сумму S_n можно записать в виде S_n = (u₁ – u₂) + (u₃ – u₄) +. . . +(u_n–1 – u_n).

Каждая из скобок, в силу условия (6), положительна или равна 0. Следовательно, S_n > 0 и является возрастающей величиной с возрастанием n.

Перегруппируем слагаемые S_n.

S_n = u₁ - (u₂ – u₃) – (u₄ – u₅) – . . . – (u_n–2 – u_n–1) – u_n = u₁ – [(u₂ – u₃) + (u₄ – u₅) +. . . +(u_n–2 – u_n–1). + u_n].

Отсюда видно, что S_n < u₁, т.е. из u₁ вычитается положительное число, причем такое, что S_n остается положительным. Итак, S_n, монотонно возрастая, остается ограниченной переменной величиной (S_n < u₁).

Следовательно, на основании признака Вейерштрасса существует предел S_n, причем ясно, что 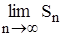= S £ u₁.

Докажем теперь признак Лейбница для n – нечетного. Тогда S_n = S_n–1 + u_n, где n – 1 –четное число. Так как 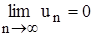и 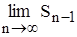= S £ u₁ (по доказанному), то и 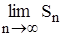также существует, причем

,

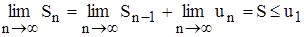что и требовалось доказать.

Оценка остатка сходящегося знакочередующегося ряда. Если знакочередующийся ряд сходится по признаку Лейбница, то его n–й остаток по абсолютной величине не превосходит первого из отброшенных членов.

Доказательство.

Пусть дан ряд u₁ – u₂ + u₃ – u₄ + . . . (–1)ⁿ⁺¹u_n +. . . , который сходится по признаку Лейбница. Тогда n–й остаток ряда R_n = ± (u_n+1 – u_n+2 + u_n+3 . . . ) сам является суммой знакочередующегося ряда. На основании признака Лейбница остаток R_n, т.е. сумма по абсолютной величине должна быть не больше первого отброшенного члена ряда, т.е.

|R_n| £ u_n+1.

Пример. Вычислить с точностью до 0,01 сумму ряда

.

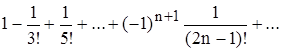Решение

1. Установим:

а) ряд знакочередующийся:

б) 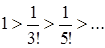; в) .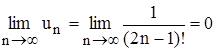

Следовательно, ряд сходится по признаку Лейбница. Найдем сумму ряда с точностью до 0,01. Так как сумма должна быть вычислена с точностью до 0,01, то достаточно, чтобы выполнялось неравенство |R_n| £ u_n+1 £ 0,01 или 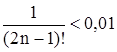, т.к. .

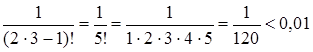Итак, .

Определение. Знакопеременный ряд u₁ + u₂ + . . . u_n +. . . называется абсолютно сходящимся, если сходится сам ряд и ряд, составленный из абсолютных величин его членов |u₁| + |u₂| + . . . |u_n | +. . .

Определение. Знакопеременный ряд u₁ + u₂ + + . . . u_n +. . . называется неабсолютно (условно) сходящимся, если он сходится, а ряд, составленный из абсолютных величин его членов, расходится.

Теорема Дирихле.(Дирихле Петер Густав 1805-1859). Сумма абсолютно сходящегося ряда не меняется от любой перестановки его членов.

Теорема Римана. (Риман Георг Фридрих Бернард 1826-1866). Если ряд условно сходится, то перестановка членов может изменить его сумму или даже сделать ряд расходящимся.

Порядок исследования знакочередующегося ряда на сходимость.

1. Установить чередование знака и убывание членов ряда по абсолютной величине.

2. Найти .

3. Сделать вывод по признаку Лейбница.

4. Составить ряд из абсолютных величин и исследовать его на сходимость.

Замечание. Убывание членов ряда по абсолютной величине может наблюдаться, начиная с некоторого числа ряда.