Главная | Обратная связь

Необходимое условие разложения. Единственность разложения

Из теоремы 1 следует, что для разложения функции f(x) в ряд Тейлора необходимо, чтобы функция была дифференцируема бесконечное число раз. Таким образом, необходимым условием разложимости функции в ряд Тейлора является наличие у функции f(x) производных всех порядков.

Если функция разложима в степенной ряд, то в соответствии с теоремой 1 коэффициенты в разложении определяются по формулам (4). В этом и заключается единственность разложения.

Достаточные условия разложения функции в ряд определяются следующей теоремой.

Теорема 2.Пусть функция f(x) имеет производные всех порядков. Для того, чтобы функция f(x) в некотором промежутке (а – R, а + R) являлась суммой составленного для нее ряда Тейлора, т. е. разлагалась в ряд Тейлора, необходимо и достаточно, чтобы остаточный член R_n(x) формулы Тейлора для этой функции стремился к нулю при n ® ¥ для всех х из указанного промежутка.

Доказательство.

Пусть f(x) есть сумма ряда Тейлора, а

его n-я частичная сумма, тогда имеет место формула Тейлора

.

Отсюда R_n(x) = f(x) – s_n(x),

,

но т. к. 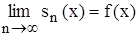, то получается, что .

Теорема доказана.

Возникает вопрос, справедливо ли обратное утверждение? То есть, если функция f(x) бесконечно дифференцируема на интервале [a – R; a + R], где

R ¹ 0, и для нее формально построен ряд Тейлора

f(x) = а₀ + а₁ (х – a) + а₂ (х – a)² + . . . + a_n (х – a)ⁿ + . . . ,

то будет ли он сходиться на интервале [a – R; a + R] и, если да, то будет ли его сумма равна функции f(x)? В общем случае ответ на этот вопрос является отрицательным, как показывает пример функции

Эта функция бесконечно дифференцируема на всей оси х, причем в начале координат

f(0) = f¢(0) = f²(0) =. . . = f⁽ⁿ⁾(0) = fⁿ⁺¹⁾(0) = . . .= 0.

Следовательно, все коэффициенты ряда Тейлора для этой функции равны нулю, ряд Тейлора сходится на всей оси Х, и его сумма тождественно равна нулю, в то время как данная функция равна нулю только в начале координат.

Таким образом,стремление к нулю остаточного члена формулы Тейлора для функции обеспечивает возможность разложения ее в степенной ряд. На практике убедиться в стремлении к нулю остаточного члена формулы Тейлора для заданной функции бывает сложно.

Существует простой достаточный признак условия разложения функции в степенной ряд, который мы сформулируем в виде теоремы.

Теорема 3. Если в некотором промежутке изменения аргумента х функция f(x) имеет производные всех порядков и эти производные по абсолютной величине ограничены одним и тем же постоянным числом:

, (6)

то составленный для f(x) ряд Тейлора сходится к f(x) в указанном промежутке.

Доказательство.

Запишем остаточный член формулы Тейлора в так называемой форме Лагранжа: 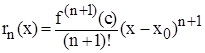, где с – некоторое промежуточное число, лежащее между х и х₀.

Ввиду (6) для него получим оценку

.

Выражение является общим членом сходящегося ряда с положительными членами и поэтому ® 0 при n ® ¥ при любом х из указанного промежутка.

Следовательно, и в силу теоремы 2 ряд Тейлора сходится к f(x) в рассматриваемом промежутке.