Главная | Обратная связь

Степенные ряды. Теорема Абеля

Из функциональных рядов наибольший интерес представляют степенные и тригонометрические ряды. Вначале рассмотрим степенные ряды.

Определение. Степенным называется ряд вида

а₀ + а₁(х – а) + а₂(х – а)² + . . . + а_n (х – а)ⁿ +. . . = , (2)

где а_о, а₁, а₂, . . . а_n . . . – постоянные числа.

Если а = 0, то получим степенной ряд вида

а₀ + а₁х + а₂х² + . . . + а_n хⁿ +. . . = . (3)

Ряд (2) можно свести к ряду (3) с помощью подстановки х – а = t. Поэтому достаточно изучить ряд вида (3). Вопрос о строении области сходимости степенного ряда решает теорема Абеля.

Теорема 6 (Абеля).

1. Если степенной ряд сходится при некотором значении х = х₀ ¹ 0, то он абсолютно сходится при всяком значении х, для которого |x| < |x₀|.

2. Если степенной ряд расходится при некотором значении х = х₀ ¹ 0, то он расходится при любом х, для которого |x| > |x₀|.

Доказательство 1

Так как х₀ – точка сходимости ряда (3), то числовой ряд

а₀ + а₁х₀ + а₂х₀² + . . . + а_n х₀ⁿ +. . . (4)

сходится, что означает а_n х₀ⁿ ® 0 при n ® ¥, значит существует такое М > 0, что будет выполняться

|а_n х₀ⁿ| < M (n = 0, 1. . .) т.е. |а₀| < M, |а₁х₀| < M, |а₂х₀²| < M . . . . (5)

Перепишем ряд (4) в виде

, (6)

и рассмотрим ряд из абсолютных величин его членов

. (7)

Используя ряд (5) составим новый ряд

. (8)

При |x| < |x₀| будем иметь 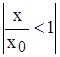и ряд (8) будет сходиться как ряд, числами которого служат члены геометрической прогрессии. Так как члены ряда (7) меньше членов ряда (8), то ряд (7) сходится по признаку сравнения. А это означает, что ряд (6), т. е. ряд (3) абсолютно сходится, что и требовалось доказать.

Доказательство 2 (от противного).

Пусть в некоторой точке х₁, удовлетворяющей неравенству |x₁| > |x₀|, ряд (3) сходится. Тогда по доказанному ряд (3) будет сходится при любом х, удовлетворяющем |x| < |x₁|, в т. ч. и при х = х₀, что противоречит условию.

Итак, нет точки x₁, для которой |x₁| > |x₀|, в которой ряд (3) сходится. Что и требовалось доказать.

Структура областей сходимости – расходимости степенного ряда изображена на рис. 1.

Рис. 1

Следствия из теоремы Абеля.

1. Если х₀ ¹ 0 – точка сходимости степенного ряда (3), то (–|x₀|; |x₀|) –

интервал сходимости степенного ряда, симметричный относительно х = 0.

2. Для каждого степенного ряда существует такое число R > 0, что для всех х, для которых |x| < R, ряд сходится и для всех |x| > R ряд расходится. R – называется радиусом сходимости; (–R; R) – интервал сходимости.

На рис. 2 показаны радиус и интервал сходимости степенного ряда.

Рис. 2

Точки на концах интервала сходимости х = R, х = – R исследуются особо. В этих точках ряд может как сходиться, так и расходиться.

Таким образом, областью сходимости степенного ряда может быть интервал, полуинтервал, отрезок.

Характер сходимости степенного ряда характеризуется следующей теоремой.

Теорема 7. На всяком отрезке, целиком принадлежащем интервалу сходимости, степенной ряд сходится равномерно.

Из равномерной сходимости степенных рядов и теорем 2 – 4 о равномерно сходящихся функциональных рядах вытекают следующие свойства степенных рядов: ряды, полученные почленным дифференцированием и интегрированием степенного ряда, имеют тот же интервал сходимости и их сумма внутри интервала сходимости равна соответственно производной и интегралу от суммы первоначального ряда.

Операции почленного дифференцирования и интегрирования можно производить над степенным рядом сколько угодно раз. Следовательно, сумма степенного ряда внутри его интервала сходимости является бесконечно дифференцируемой функцией.