 |
|
Понятие предиката. Операции над предикатами.
Рассмотрим предложение: «Река х впадает в Азовское море». Оно не является высказыванием, так как не известно о какой реке идет речь. Если в этом предложении букву х заменить словом «Кубань», то получится истинное высказывание. Если же х заменить словом «Волга», то получится ложное высказывание.
Букву х в рассмотренном предложении, вместо которой можно подставить название любой реки, называют переменной. Вообще, переменной называют букву или любой символ, служащие для обозначения произвольного элемента некоторого вполне определенного множества, называемого областью изменения (или значений) переменной.
Всякое повествовательное предложение, содержащее одну или несколько переменных, которое превращается в высказывание при подстановке вместо переменных конкретных их значений, называют предикатом или высказывательной формой. При этом предикаты, зависящие от одной переменной, называют одноместными, а зависящие от двух, трех и т. д. переменных — двухместными, трехместными и т. д.
Одноместные предикаты обозначают символами А(х), В(у), Р(у), Q(х) и т. д. Аналогично, Р (х; у), Q (y; z) — двухместные предикаты и т.д.
Совокупность значений переменных, входящих в данный предикат Р, при которых этот предикат имеет смысл, называют областью определения предиката Р и обозначают Dp.
Множество значений переменных из Dp, при которых предикат Р превращается в истинное высказывание, называется областью истинности предиката Р и обозначается Up. Все значения, не вошедшие в описанную область, составляют области ложности предиката.
Примерами одноместных предикатов являются уравнения и неравенства с одной переменной. Областями истинности таких предикатов являются множества решений этих уравнений, неравенств.
Предикат Р называется тождественно истинным (ложным), если область определения предиката совпадает с областью истинности (ложности).
Так как предикаты при конкретных значениях переменных превращаются в высказывания, то над ними можно производить такие же логические операции, как и над высказываниями.
Кванторы.
Рассмотрим следующий предикат Р(х): «Река х впадает в Азовское море». Этот предикат превращается в высказывание не только тогда, когда вместо х подставлено название какой-либо реки, но и тогда, когда перед этой переменной поставлено одно из слов: «любая» или «существует». В самом деле, предложения
а) «Любая река х впадает в Азовское море» и
б) «Существует река х, впадающая в Азовское море» являются высказываниями, причем первое из них ложно, а второе истинно.
Если через X обозначить множество рек на Земле, то эти высказывания в символической форме можно записать следующим образом:
а)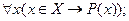 
б) 
Здесь символ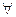 
—это перевернутая первая буква английского слова «All», означающий «все», и называют его квантором всеобщности» а символ 
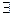— перевернутая первая буква английского слова «Exists», означающий «существует», «найдется», и называют его квантором существования.
Заметим, что предложения а) и б) уже не являются предикатами, они не зависят ни от какой переменной: говорят, что здесь х — связанная переменная. Записи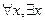 
называют операциями навешивания кванторов на переменную х. Кванторы 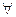, 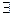называют двойственными.
Пусть теперь Р (х) произвольный одноместный предикат, определенный на множестве X. Тогда будем употреблять краткие обозначения, представленные в табл. 3.
Таблица 3.
| Обозначение | Прочтение |
 )
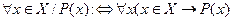| Для любого элемента x из множества X выполняется условие P(x). Все элементы xÎX обладают свойством P(x). |
| Существует элемент xÎX, обладающий свойством P(x). Найдется хотя бы один элемент xÎX, который удовлетворяет условию P(x). |
Например, запись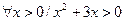 
означает, что для любого положительного числа х справедливо неравенство 
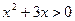. Ясно, что это истинное высказывание. Однако, высказывание 
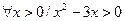уже ложно.
Запись 
означает, что найдется хотя бы одно положительное число, удовлетворяющее уравнению 
.
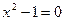Операция навешивания квантора всеобщности (существования) на переменную есть обобщение операции конъюнкции (дизъюнкции) на любое множество высказываний.
Кванторы всеобщности и существования, как и операции конъюнкции и дизъюнкции, связаны соотношениями де Моргана. А именно, справедливы следующие равносильности:
;
.
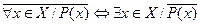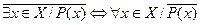Операцию навешивания квантора на переменную, от которой зависит предикат, будем называть квантификацией предиката по этой переменной.
Пусть Р (х1, x2, ..., хn ) — n-местный предикат, где nÎN\l. Тогда на любую переменную х1, x2, ..., хn можно навесить квантор. Если, например, на х1 навесить квантор, то получим n-1- местный предикат 
или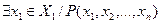 
, зависящий от переменных х2, x3, ..., хn. При этом х1 называют связанной переменной, а х2, x3, ..., хn — свободными переменными. Чтобы n-местный предикат превратить в высказывание, достаточно на каждую переменную навесить квантор, т. е. квантифицировать предикат по всем переменным.
Рассмотрим подробнее случай двухместного предиката Р (х; у). Квантифицируя его по переменной х и у, можно образовать восемь высказываний:
| 1. |  ;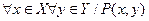
| |  ;
|
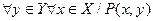| 2. |  ;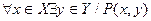
| |  ;
|
| 3. |  ;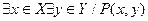
| |  ;
|
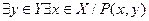| 4. |  ;
| |  .
|
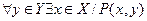Остановимся на том, как следует читать высказывания (1) — (8).
(1) — Для любого элемента х из множества X и для любого элемента у из Y выполняется условие Р (х; y).
(2) — Для каждого хÎХ найдется такое yÎY, что выполняется условие Р(х;у). Подчеркнем, что здесь yÎY может зависеть от выбранного хÎХ, т.е. для каждого отдельно взятого хÎХ найдется свое yÎY.
(3) — Существует такое хÎХ и существует такое yÎY, что выполняется условие Р(х;у) (или, которые удовлетворяют условию Р (х; у)).
(4) — Существует (найдется) такое хÎХ, что для любого yÎY выполняется условие Р(х;у).
Аналогично прочтение и остальных высказываний.
Очевидно, что высказывания (1) и (5), а также (3) и (7) имеют одинаковый смысл, следовательно, (1)Û(5) и (3)Û(7), т. е. если перед двумя соседними переменными стоят одинаковые кванторы, то эти переменные можно менять местами. Однако, соседние переменные, перед которыми стоят разноименные кванторы менять местами нельзя, или еще говорят, что разноименные кванторы менять местами нельзя. Так, высказывания (2) и (6), а также (4) и (8), имеют разный смысл, поэтому они не равносильны. Однако, справедливы следования (6) Þ (2) и (4) Þ (8), но обратные следования, вообще говоря, неверны.
Например, высказывание истинно, так как для всякого действительного числа х существует ему противоположное число у=-х. Но высказывание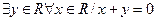 
ложно, поскольку ясно, что нет такого числа у которое было бы противоположным любому числу х.
Если Х = Y, то высказывания (1) и (3) будем записывать короче: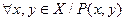 
, 
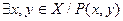. При этом читать их будем так: «для любой пары элементов х и у из множества X выполняется условие Р (х; у)»; «найдется хотя бы одна пара элементов х и у из множества X, для которых справедливо Р(х; у)».
При построении отрицаний высказываний, содержащих несколько кванторов, справедливы следующие равносильности:
;
;
;
.
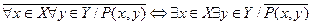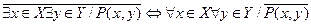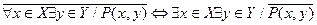Таким образом, для построения отрицания высказывания, начинающегося с кванторов, достаточно каждый квантор заменить ему двойственным, а знак отрицания перенести на предикат, стоящий за кванторами.
Наряду с квантором $ в математике часто употребляют символ $! который читают как «существует единственный». Например, запись
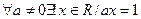
означает, что для любого, не равного нулю, действительного числа а существует единственное число х, удовлетворяющее уравнению ах = 1.