Главная | Обратная связь

Соотношение между множествами и составными высказываниями

Существует тесная связь между множествами — с одной стороны, и высказываниями — с другой, а также между операциями над множествами, с одной стороны, и операциями образования составных высказываний — с другой.

Пусть X, Y, Z,... некоторые высказывания, и пусть U — их множество логических возможностей. Пусть А, В, С,... подмножества U, для которых истинны соответственно высказывания X, Y, Z,.... Тогда А, В, С,... называются соответственно множествами истинности высказываний X, Y, Z,....

Если X и Y — высказывания, то ХÙY и ХÚY также высказывания, следовательно, они должны иметь множества истинности. Чтобы найти множество истинности высказывания ХÚY, необходимо поставить в соответствие логические возможности, которые лежат в А или в В (или в них обоих); то есть, поставить в соответствие ХÚY множество AÈB. С другой стороны, высказыванию ХÙY можно поставить в соответствие множество АÇВ.

Итак, существует тесная связь между логической операцией дизъюнкции и операцией объединения множеств, а также между конъюнкцией и пересечением. А также между логической операцией отрицания и операцией разности множеств, т. е. множеством истинности для будет .

Связь между высказыванием и его множеством истинности создает возможность «перевода» любой задачи, относящейся к составным высказываниям, в задачу теории множеств. Возможно также и обратное: если поставлена какая-то задача, касающаяся множеств, то универсальное множество можно себе представить как некоторое множество логических возможностей, подмножества которого являются множествами истинности некоторых высказываний. Следовательно, задачу, относящуюся к множествам, можно также «перевести» на язык составных высказываний.

Мы рассмотрели такие множества истинности составных высказываний, которые образованы посредством связок Ø, Ù, Ú. Все остальные связки можно определить через эти три основные и тем самым вывести, какие множества истинности им соответствуют.

Таким образом, два высказывания эквивалентны тогда и только тогда, когда они имеют одни и те же множества истинности. Заметим, что диаграммы Эйлера-Венна помогают обнаруживать отношения между высказываниями.

Предположим теперь, что X — логически истинное высказывание. Поскольку высказывание X логически истинно тогда и только тогда, когда оно истинно в каждом логически возможном случае, множеством истинности для высказывания X должно быть универсальное множество U. Подобным же образом, если высказывание X логически ложно, то оно ложно в каждом логически возможном случае, и поэтому его множеством истинности будет пустое множество Æ.

Рассмотрим отношение следствия, реализуемое операцией импликации. Высказывание X ®Y тогда и только тогда логически истинно, когда его множество истинности совпадает с U, т. е. и A\B = Æ. Но если A\B пусто, то В включает в себя А. Отношение включения читается «А является подмножеством В». Таким образом, высказывание X ®Y логически истинно тогда и только тогда, когда АÌВ.

Таким образом, каждому высказыванию соответствует его множество истинности, каждой логической связке соответствует операция над множеством. Каждому отношению между высказываниями соответствует отношение между множествами истинности. Множествами истинности высказываний ХÚY, ХÙY, и X ®Y служат соответственно:

AÈB, АÇВ, ,

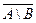
Высказывание X логически истинно, если А = U, и логически ложно, если А =Æ. Высказывание X и Y эквивалентны тогда и только тогда, когда А = В; из X следует Y тогда и только тогда, когда АÌВ.