 |
|
Задания для самостоятельной работы по теме 1.
Задание 1. Построить таблицу истинности для заданной формулы. Определить для каждого высказывания, будет ли оно логически истинным, противоречивым или ни тем ни другим.
| 1. | Ф=A®(B®A) | | Ф=(A®B)Ú(B®`A) |
| 2. | Ф=AÙ`BÙC | | Ф=(`AÚ(BÙC))®B |
| 3. | Ф=C®(A®(BÚA)) | | Ф=((AÙB)®C)Ù(CÚ`B) |
| 4. | Ф=(AÙB)®C | | Ф=(C®B)®A)®(CÚB) |
| 5. | Ф=C®((AÚB)ÚC) | | Ф=((A®B)Ú(B®C))«((CÙB)®(AÙ`C)) |
| 6. | Ф=((AÚB)Ù(AÙ`B))«C | | Ф= 
|
| 7. | Ф= (XÚY) «(XÙY) | | Ф= 
|
| 8. | Ф=(X®Y)®(Y®`X) | | Ф=(X®Y) Ù (Y®Z) Ù 
|
Задание 2. Определить, является ли заданная формула тождественно истинной.
| 1. | Ф=(P®Q)Ú(Q®P); | | Ф=(PÙQ)®P |
| 2. | Ф=P®(Q®(PÚQ)); | | Ф=P®(PÚQ) |
| 3. | Ф=  ;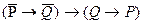
| | Ф= 
|
Задание 3. Доказать равносильность заданных логических формул (двумя способами: с помощью таблицы истинности и используя основные законы логических операций).
| 1. | 
|
| 2. | 
|
| 3. |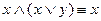 
|
| 4. |  = 
|
| 5. |  =A
|
| 6. |  =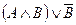 
|
| 7. | 
|
| 8. | 
|
| 9. | 
|
| 10. | 
|
| 11. | 
|
| 12. |  =A
|
| 13. | 
|
| 14. |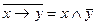 
|
| 15. | 
|
| 16. | 
|
Задание 4. Применяя равносильные преобразования, упростить формулы.
| | 
| 8. | 
|
| | 
| 9. | 
|
| | 
| 10. | 
|
| | 
| 11. | 
|
| | 
| 12. | 
|
| | 
| 13. | 
|
| | 
| 14. |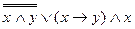 
|
| | 
| 15. |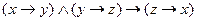 
|
| | 
| 16. | 
|
| | 
| 17. | 
|
Задание 5. Определить, являются ли приведенные ниже формулы тождественно-истинными? Проверку выполнить двумя способами: построив таблицу истинности и упростив выражения.
| | 
| 4. | 
|
| | 
| 5. | 
|
| | 
| 6. |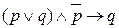 
|
Задание 6. 
Пусть X означает: «Я сдам этот экзамен»; а Y: «Я буду регулярно выполнять домашние задания». Запишите в символической форме следующие высказывания:
(а) «Я сдам этот экзамен только в том случае, если буду регулярно выполнять домашние задания».
б) «Регулярное выполнение домашних заданий является необходимым условием для того, что я сдам этот экзамен».
(в) «Сдача этого экзамена является достаточным условием того, что я регулярно выполнял домашние задания».
(г) «Я сдам этот экзамен в том и только в том случае, если я буду регулярно выполнять домашние задания».
(д) «Регулярное выполнение домашних заданий есть необходимое и достаточное условие для того, чтобы я сдал этот экзамен».
Выясните, какому из перечисленных высказываний соответствуют следующие символические формы: Х®Y; Y «X; Y®X.
Задание 7. Решить задачу, составив логическую формулу.
1.В одном королевстве были незамужние принцессы, голодные тигры и приговоренный к казни узник. Всякому узнику, осужденному на смерть, король давал последний шанс. Узнику предлагалось угадать, в какой из двух комнат находится тигр, а в какой принцесса. Хотя вполне могло быть, что король в обеих комнатах разместил принцесс или тигров. Выбор надо было сделать на основании табличек на дверях комнаты. Известно, что утверждения на табличках были либо оба истинными, либо оба ложными. Надписи гласили:
| 1 комната | 2 комната |
| По крайней мере, в одной из этих комнат находится принцесса | Тигр сидит в первой комнате |
Какую дверь должен выбрать узник?
2.На соревнованиях по легкой атлетике Андрей, Борис, Сергей и Володя заняли первые четыре места. Но когда однокурсницы стали вспоминать, как эти места распределились между победителями, то мнения разошлись. Даша сказала: «Андрей был первым, а Володя – вторым». Галя утверждала: «Андрей был вторым, а Борис – третьим». Лена считала: «Борис был четвертым, а Сергей – вторым». Ася, которая была судьей на этих соревнованиях и хорошо помнила, как распределились места, сказала, что каждая из девушек сделала одно правильное и одно неправильное заявление. Кто из студентов занял первое, второе и третье место?
3.Студент делает следующие высказывания: А. Если я люблю физику, то люблю и математический анализ. Б. Если высказывание A истинно, то я люблю физику. Следует ли из этих высказываний, что студент любит физику?
4.Юра условился с родителями, что всегда будет говорить им только правду. Однажды он получил 2 по физике и очень не хотел говорить об этом дома. На прямой вопрос, что он получил по физике, Юра ответил… Что же ответил Юра так, чтобы не сказать о двойке, и в то же время сказать совершеннейшую истину?
Задание 8. Преобразовать формулы так, чтобы они содержали только операции конъюнкции и отрицания:
1) 
| 2) 
|
3) 
| 4) 
|
5) 
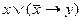
| 6) 
|
7) 
| 8) 
|
9) 
| 10) 
|
Задание 9. Преобразовать формулы так, чтобы они содержали только операции дизъюнкции и отрицания.
1) 
| 2) 
|
3) 
| 4) 
|
5) 
| 6) 
|
7) 
| 8) 
|
Задание 10. Какие из следующих предложений являются предикатами?
1) x делится на 3  ;
| 2) x делится на 5 ;
|
3) 
| 4) 
|
5) 
| 6) 
|
7) 
| 8)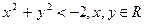 
|
Задание 10. На множестве натуральных чисел заданы два предиката:
P(x) – «число 3 делитель x»;
Q(x) – «x£6».
Найдите множества истинности следующих предикатов:
| 1. | 
| 3. | 
|
| 2. | 
| 4. | 
|
Задание 11. Предикат P(x): «x есть рациональное число»; предикат Q(x): «x есть действительное число»; предикат T(x): « x меньше y». Запишите следующие утверждения, используя кванторы:
1) каждое рациональное число есть действительное число;
2) существует число, которое является простым;
3) для каждого числа x существует такое число y, что x меньше y.
Задание 12. Определить, для каких натуральных значений переменных x1, x2 заданный предикат принимает значение истина:
| 1) | 
|
| 2) | 
|
| 3) | 
|
| 4) | 
|
| 5) |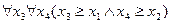 
|
Задание 13. Составить предикат для натуральных чисел, выразив его с помощью арифметических отношений и логических связок, который принимает значение истина тогда и только тогда, когда:
1) x1 в два раза больше x2;
2) если x1>0, то для всех x3< x2 найдутся такие x4, что x4+1£ x1;
3) для всех x1 и x2, если x1£x2 и x2<x3, то x1<x3;
4) для всех x1 и x2, если x1£x2 и x2£x1, то x1=x2;
5) для всех x1 и x2, если неверно, что x1<x2 или x3<x2, то x1³x2 и x3³x2.
Задание 14. Ввести необходимые предикаты и с помощью кванторов записать следующие определения, с помощью законов де Моргана получить их отрицания:
1) определение предела числовой последовательности;
2) определение фундаментальной по Коши последовательности;
3) определение предела функции в точке;
4) определение непрерывности функции в точке;
5) определение непрерывной на интервале функции;
6) определение равномерно непрерывной на интервале функции.
Контрольные вопросы по теме 1.
1) Приведите примеры высказываний (истинных и ложных) и предложений, не являющихся высказываниями.
2) Является ли высказывание "неверно, что 6 делится на 3" простым?
3) Покажите на примере, что значение истинности составного высказывания зависит от типа связок, участвующих в образовании составного высказывания.
4) Подсчитайте количество логических возможностей формулы от 3-х высказывательных переменных, 4-х высказывательных переменных.
5) Перечислите общие логические возможности формул
и 
6) Дайте словесное определение операциям Ø, Ù, Ú, ®, «.
7) Известно, что высказывание А®В истинно. Что можно сказать об истинности высказываний А и В?
8) Известно, что высказывание А®В ложно. Что можно сказать об истинности А и В?
9) Известно, что А®В иА истинны. Что можно сказать об истинности В?
10) А « В истинно. Что можно сказать об истинности формул ØА« В и А® В?
11) АÙØВ и А« В ложны. Что можно сказать об истинности А и В?.
12) В трехместную высказыватсльную форму вместо двух неизвестных поставили конкретные значения. Какова «местность» полученной высказывательной формы?
13) В чем различие между высказывательными формами и предикатами?
14) Чем отличается предикат от предикатной переменной?
15) Записать одноместный предикат на множестве N. область истинности которого состоит из всех нечетных чисел.
16) Определить «местность» предикатов:
· P(x)ÚQ(x,y);
· Р(х)ÙQ(y);
· P(x.y.z)®Q(x,t);
· P(x.y,z)«Q(y);
· ØP(x,y,z).
17) Пусть P(x) = «x делится на l», Q(y)= «1 делится на y» — предикаты, заданные на множестве натуральных чисел. Определить истинность следующих высказываний:
$x P(x); "x P(x); $y Q(y); "y Q(y).
18. Пусть P(x,y,z) = «x*(y*z) = (x*y)*z», Q(x,y,z) = «x — (y — z) = (x — у) — z» - предикаты на множестве целых чисел. Определить истинность высказываний:
· "x"y"z Р(х, у, z);
· "x"y"z Q(x,y,z);
· $x$y$zQ(x,y,z);
· "x$y$zQ(x,y.z);
· "x$z"yQ(x,y,z).